��Ŀ����
17�����ں���y=$\frac{3}{a}$x2+��3-$\frac{2}{a}$��x+1-$\frac{1}{a}$��a��0�����������н��ۣ��ٵ�a=2ʱ���ú����Ķ�������Ϊ��-$\frac{2}{3}$��-$\frac{1}{6}$����
�ڵ�a��0ʱ���ú���ͼ��ͬһ�㣻
�۵�a��0ʱ������ͼ���x�������߶γ��ȴ���$\frac{4}{3}$��
�ܵ�a��0ʱ��������x��$\frac{1}{3}$ʱ��y��x�����������
������ȷ�Ľ����Т٢ڢۢܣ���д���ż��ɣ�
���� ��a=2����y=$\frac{3}{a}$x2+��3-$\frac{2}{a}$��x+1-$\frac{1}{a}$������ú����Ķ������꼴���жϣ���x=1����y=$\frac{3}{a}$x2+��3-$\frac{2}{a}$��x+1-$\frac{1}{a}$=4���Ӷ��ж�����ͼ��ͬһ�㣨1��4����������x��Ľ��������ϵ���Ĺ�ϵ�����ж�ͼ���x�������߶γ��ȣ�ͨ����öԳ���x=-$\frac{3-\frac{2}{a}}{2��\frac{3}{a}}$=-$\frac{a}{2}$+$\frac{1}{3}$�������жϺ��������ʣ�
��� �⣺��a=2����y=$\frac{3}{a}$x2+��3-$\frac{2}{a}$��x+1-$\frac{1}{a}$�ã�y=$\frac{3}{2}$x2+2x+$\frac{1}{2}$=$\frac{3}{2}$��x+$\frac{2}{3}$��2-$\frac{1}{6}$��
�ඥ�����꣨-$\frac{2}{3}$��-$\frac{1}{6}$�����ʢ���ȷ��
��x=1����y=$\frac{3}{a}$x2+��3-$\frac{2}{a}$��x+1-$\frac{1}{a}$=4��
��a��0ʱ������y=$\frac{3}{a}$x2+��3-$\frac{2}{a}$��x+1-$\frac{1}{a}$��a��0��ͼ��һ��������1��4���㣬�ʢ���ȷ��
�躯��y=$\frac{3}{a}$x2+��3-$\frac{2}{a}$��x+1-$\frac{1}{a}$��a��0����ͼ����x��Ľ���Ϊ��x1��0������x2��0����
�������⣺x1+x2=-$\frac{3-\frac{2}{a}}{\frac{3}{a}}$=-a+$\frac{2}{3}$��x1x2=$\frac{1-\frac{1}{a}}{\frac{3}{a}}$=$\frac{a}{3}$-$\frac{1}{3}$��
�ߣ�x1-x2��2=��x1+x2��2-4x1x2=��-a+$\frac{2}{3}$��2-4��$\frac{a}{3}$-$\frac{1}{3}$��=a2-$\frac{8}{3}$a+$\frac{16}{9}$��
��a��0ʱ��a2-$\frac{8}{3}$a��0��
�൱a��0ʱ���ߣ�x1-x2��2��$\frac{16}{9}$��
��|x1-x2|��$\frac{4}{3}$��
�ຯ��ͼ���x�������߶γ��ȴ���$\frac{4}{3}$���ʢ���ȷ��
�ߺ���y=$\frac{3}{a}$x2+��3-$\frac{2}{a}$��x+1-$\frac{1}{a}$��a��0���ĶԳ���x=-$\frac{3-\frac{2}{a}}{2��\frac{3}{a}}$=-$\frac{a}{2}$+$\frac{1}{3}$��
�൱a��0ʱ���������ϣ���x��$\frac{1}{3}$��
�ຯ����x��$\frac{1}{3}$ʱ��y��x����������ʢ���ȷ��
�ʴ�Ϊ�٢ڢۢܣ�
���� ���⿼���˶��κ����������Լ����κ���ͼ���ϵ�������������������ն��κ����������ǽ���Ĺؼ���

 ������ϵ�д�
������ϵ�д�| A�� | 16 | B�� | 8 | C�� | 4 | D�� | 2 |
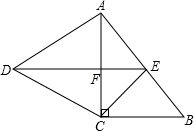 ��ͼ����Rt��ABC�У���ACB=90�㣬��ACΪһ���������ȱ�������ACD����EΪAB���е㣬����DE����AC�ཻ�ڵ�F��
��ͼ����Rt��ABC�У���ACB=90�㣬��ACΪһ���������ȱ�������ACD����EΪAB���е㣬����DE����AC�ཻ�ڵ�F��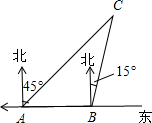 ��ͼ����A��B���Ҵ��ڴ��к��У�B����A����������������������20����ľ��룬ijһʱ�������Ҵ�ͬʱ�����A�Ķ�������B�ı�ƫ��15�㷽������һ�Ҵ�C����ô��ʱ��C�봬B�ľ�����20$\sqrt{2}$�������������ţ���
��ͼ����A��B���Ҵ��ڴ��к��У�B����A����������������������20����ľ��룬ijһʱ�������Ҵ�ͬʱ�����A�Ķ�������B�ı�ƫ��15�㷽������һ�Ҵ�C����ô��ʱ��C�봬B�ľ�����20$\sqrt{2}$�������������ţ���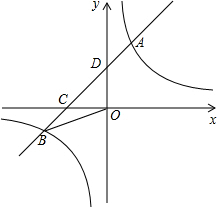 ��ͼ����ƽ��ֱ������ϵ�У�һ�κ���y=ax+b�뷴��������y=$\frac{k}{x}$��ͼ����һ��������A��B���㣬��x�ύ�ڵ�C����y�ύ�ڵ�D����֪��B������Ϊ��-5��-2����CΪBD���е㣮
��ͼ����ƽ��ֱ������ϵ�У�һ�κ���y=ax+b�뷴��������y=$\frac{k}{x}$��ͼ����һ��������A��B���㣬��x�ύ�ڵ�C����y�ύ�ڵ�D����֪��B������Ϊ��-5��-2����CΪBD���е㣮