题目内容
如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3).
(1)请画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标;
(2)请画出△ABC绕点B逆时针旋转90°后的△A2BC2;
(3)求出(2)中C点旋转到C2点所经过的路径长(结果保留根号和π).


【考点】作图-旋转变换;弧长的计算;作图-轴对称变换.
【专题】作图题.
【分析】(1)利用关于x轴对称点的横坐标相等,纵坐标化为相反数可先找出点A1、B1、C1的坐标,然后画出图形即可;
(2)利用旋转的性质可确定出点A2、C2的坐标;
(3)利用弧长公式进行计算即可.
【解答】解:(1)根据关于x轴对称点的坐标特点可知:A1(2,﹣4),B1(1,﹣1),C1(4,﹣3),
如图下图:连接A1、B1、C1即可得到△A1B1C1.


(2)如图:


(3)由两点间的距离公式可知:BC=
 ,
,
∴点C旋转到C2点的路径长=
 .
.
【点评】本题主要考查的是图形的对称、图形的旋转以及扇形的弧长公式,掌握相关性质是解题的关键.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目

 的长为πcm,OD=3cm,求图中阴影部分的面积是多少?
的长为πcm,OD=3cm,求图中阴影部分的面积是多少?

 的解为正数,那么m的取值范围是 .
的解为正数,那么m的取值范围是 .


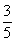 ,则cosB的值是
,则cosB的值是