题目内容
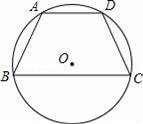
如图,四边形ABCD内接于⊙O,AD∥BC,求证:AB=CD.

【考点】圆内接四边形的性质.
【专题】证明题.
【分析】根据AD∥BC,得出∠A+∠B=180°,再根据圆内接四边形的对角互补得出∠A+∠C=180°,由同角的补角相等得到∠B=∠C,所以四边形ABCD是等腰梯形,于是AB=CD.
【解答】证明:∵AD∥BC,
∴∠A+∠B=180°,
∵四边形ABCD内接于⊙O,
∴∠A+∠C=180°,
∴∠B=∠C,
又∵AD∥BC,且AD≠BC,
∴四边形ABCD是等腰梯形,
∴AB=CD.
【点评】此题考查了圆内接四边形的对角互补的性质,平行线的性质,补角的性质,等腰梯形的判定与性质,得出∠B=∠C是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 中的x、y都扩大3倍,那么分式的值是( )
中的x、y都扩大3倍,那么分式的值是( )



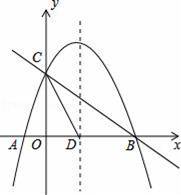
 x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).