题目内容
如果 的解为正数,那么m的取值范围是 .
的解为正数,那么m的取值范围是 .
m<1且m≠﹣3 .
【考点】分式方程的解.
【分析】先解关于x的分式方程,求得x的值,然后再依据“解是正数”建立不等式求m的取值范围.
【解答】解:去分母得,1+x﹣2=﹣m﹣x,
∴x= ,
,
∵方程的解是正数
∴1﹣m>0即m<1,
又因为x﹣2≠0,
∴ ≠2,
≠2,
∴m≠﹣3,
则m的取值范围是m<1且m≠﹣3,
故答案为m<1且m≠﹣3.
【点评】本题考查了分式方程的解,由于我们的目的是求m的取值范围,根据方程的解列出关于m的不等式,另外,解答本题时,易漏掉m≠﹣2,这是因为忽略了x﹣2≠0这个隐含的条件而造成的,这应引起同学们的足够重视.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
在一次数学课上,李老师出示一道题目:
| 如图,在△ABC中,AC=BC,AD=BD,∠A=30°,在线段AB上求作两点P,Q,使AP=CP=CQ=BQ. |
明明作法:分别作∠ACD和∠BCD的平分线,交AB于点P,Q.点P,Q就是所求作的点.
晓晓作法:分别作AC和BC的垂直平分线,交AB于点P,Q.点P,Q就是所求作的点.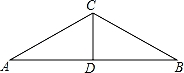
你认为明明和晓晓作法正确的是( )
A.明明 B.晓晓 C.两人都正确 D.两人都错误
 中的x、y都扩大3倍,那么分式的值是( )
中的x、y都扩大3倍,那么分式的值是( )
 ,然后在0,1,2,3中选择一个你喜欢的a值,代入求值.
,然后在0,1,2,3中选择一个你喜欢的a值,代入求值.
