题目内容
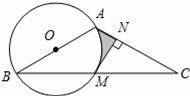
如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点M,MN⊥AC于点N.
(1)求证:MN是⊙O的切线;
(2)若∠BAC=120°,AB=2,求图中阴影部分的面积.

【考点】切线的判定;扇形面积的计算;解直角三角形.
【专题】几何综合题;压轴题.
【分析】(1)有切点,需连半径,证明垂直,即可;
(2)求阴影部分的面积要把它转化成S梯形ANMO﹣S扇形OAM,再分别求的这两部分的面积求解.
【解答】(1)证明:连接OM.
∵OM=OB,
∴∠B=∠OMB.
∵AB=AC,
∴∠B=∠C.
∴∠OMB=∠C.
∴OM∥AC.
∵MN⊥AC,
∴OM⊥MN.
∵点M在⊙O上,
∴MN是⊙O的切线.
(2)解:连接AM.
∵AB为直径,点M在⊙O上,
∴∠AMB=90°.
∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°.
∴∠AOM=60°.
又∵在Rt△AMC中,MN⊥AC于点N,
∴∠AMN=30°.
∴AN=AM•sin∠AMN=AC•sin30°•sin30°=
 .
.
∴MN=AM•cos∠AMN=AC•sin30°•cos30°=
 .
.
∴S梯形ANMO=
 ,
,
S扇形OAM=
 ,
,
∴S阴影=
 =
=
 ﹣
﹣
 .
.




【点评】本题考查的是切线的判定即利用图形分割法求不规则图形面积的思路.

练习册系列答案
相关题目
 ,然后在0,1,2,3中选择一个你喜欢的a值,代入求值.
,然后在0,1,2,3中选择一个你喜欢的a值,代入求值.


 B.
B.
 C.
C.
 D.
D.

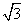 cos 30°+tan 45- 4sin260°.
cos 30°+tan 45- 4sin260°.