Question

5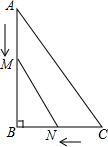．如图，在Rt△ABC中，∠B=90°，AB=8m，BC=6m，点M、点N同时由A、C两点出发分别沿AB、CB方向向点B匀速移动，它们的速度都是1m/s，几秒后，△MBN的面积为Rt△ABC的面积的$\frac{1}{2}$？

Answer 1

分析 可设x秒后，S_△MBN=$\frac{1}{2}$S_△ABC，而此时AM=CN=xm，BM=（8-x）m，BN=（6-x）m，S_△MBN=$\frac{1}{2}$×BM×BN，S_△ABC=$\frac{1}{2}$×8×6，进而可列出方程，求出答案；

解答 解：设x秒后，S_△MBN=$\frac{1}{2}$S_△ABC，
由题意得（8-x）×（6-x）×$\frac{1}{2}$=$\frac{1}{2}$×$\frac{1}{2}$×6×8，
即x²-14x+24=0，
解得：x₁=2，x₂=12（不合题意舍去），
答：当2秒后，△MBN的面积为Rt△ABC的面积的$\frac{1}{2}$．

点评 此题考查了一元二次方程的应用，这类题目体现了数形结合的思想，通常这类问题可转化为一元二次方程求解，但应注意考虑解的合理性，即考虑解的取舍．