题目内容
4. 如图,AB是⊙O的直径,E是圆上一点,OE⊥BC交BC于点D,OD=3,DE=2,求BC与AD的长.
如图,AB是⊙O的直径,E是圆上一点,OE⊥BC交BC于点D,OD=3,DE=2,求BC与AD的长.
分析 连接AC,根据题意求出⊙O的半径为5,根据勾股定理和垂径定理求出BC的长,根据三角形中位线定理求出AC=6,根据勾股定理求出AD的长.
解答 解:连接AC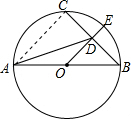 ,
,
∵OD=3,DE=2,
∴OE=5,即⊙O的半径为5,
在Rt△ODB中,BD=$\sqrt{O{B}^{2}-O{D}^{2}}$=4,
∵OE⊥BC,
∴BC=2BD=8;
∵OE⊥BC,
∴BD=DC,又BO=OA,
∴OD是△ABC的中位线,
∴AC=2OD=6,
∵AB为⊙O的直径,
∴∠C=90°,
∴AD=$\sqrt{A{C}^{2}+C{D}^{2}}$=2$\sqrt{13}$.
点评 本题考查的是垂径定理、圆周角定理和勾股定理的应用,掌握直径所对的圆周角是直角、垂直于弦的直径平分弦并且平分弦所对的弧是解题的关键.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
 如图,在Rt△ABC中,∠C=90°,AC=3,BC=4.现将线段AC沿AD折叠后,使得点C落在AB上,求折痕AD的长度.
如图,在Rt△ABC中,∠C=90°,AC=3,BC=4.现将线段AC沿AD折叠后,使得点C落在AB上,求折痕AD的长度. 如图,已知A(1,-3),B(-2,-2),C(2,0).
如图,已知A(1,-3),B(-2,-2),C(2,0).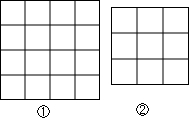 如图,每个小正方形的边长都是1,每个小格的顶点叫做格点,以格点为顶点,分别按下列要求画三角形:
如图,每个小正方形的边长都是1,每个小格的顶点叫做格点,以格点为顶点,分别按下列要求画三角形: 已知,如图,折叠长方形的一边AD,使点D落在BC边上的点F处,如AB=8,BC=10.求EC的长.
已知,如图,折叠长方形的一边AD,使点D落在BC边上的点F处,如AB=8,BC=10.求EC的长.