Question

19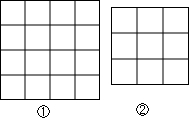．如图，每个小正方形的边长都是1，每个小格的顶点叫做格点，以格点为顶点，分别按下列要求画三角形：
（1）在图①中，画一个三角形，使它的三边长都是有理数；
（2）在图②中，画一个三边长分别为3，2$\sqrt{2}$，$\sqrt{5}$的三角形，一共可画这样的三角形16个．

Answer 1

分析 （1）画一个边长3，4，5的三角形即可；
（2）由勾股定理容易得出结果．

解答 解：（1）∵$\sqrt{{3}^{2}+{4}^{2}}$=5，
∴△ABC即为所求，
如图1所示：
（2）如图2所示：
∵$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$，$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$，
∴△ABC，△DBC，…，
都是符合条件的三角形，一共可画这样的三角形16个；
故答案为：16．

点评 本题考查了正方形的性质、勾股定理、作图--应用与设计作图；熟记勾股定理是解决问题的关键．