题目内容
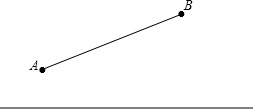 公路同侧有A、B两个村庄,相距
公路同侧有A、B两个村庄,相距| 17 |
考点:作图—应用与设计作图
专题:
分析:作点A关于公路的对称点A′,连接A′B交公路于点P,点P就是设置的站台,利用勾股定理求出AF,再运用在直角△BA′E中的勾股定理求出A′B即可.
解答:解:如图,作点A关于公路的对称点A′,连接A′B交公路于点P,点P就是设置的站台,

作BE垂直公路,A′E平行公路.
∵AB=
千米,BF=BD-AC=2-1=1千米,
∴AF=
=
=4千米,
∴A′B=
=
=5千米.

作BE垂直公路,A′E平行公路.
∵AB=
| 17 |
∴AF=
| AB2-BF2 |
| 17-1 |
∴A′B=
| A′E2+BE2 |
| 42+32 |
点评:本题主要考查了作图-应用与设计作图,解题的关键是利用轴对称性作出最短距离.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 如图是一家商场某品牌运动鞋不同码数的销售情况,你认为这家商场进货最多的运动鞋的码数会是( )
如图是一家商场某品牌运动鞋不同码数的销售情况,你认为这家商场进货最多的运动鞋的码数会是( )| A、40 | B、41 | C、42 | D、43 |
 如图,Rt△ABC中∠C=90°,D为AB的中点,分别作AE∥CB、BE∥AC,两线交于点E,连接DE.作EF∥AB交CB延长线于点F,取EF中点G,连接BG.问四边形DEGB是什么特殊四边形?说明理由.
如图,Rt△ABC中∠C=90°,D为AB的中点,分别作AE∥CB、BE∥AC,两线交于点E,连接DE.作EF∥AB交CB延长线于点F,取EF中点G,连接BG.问四边形DEGB是什么特殊四边形?说明理由.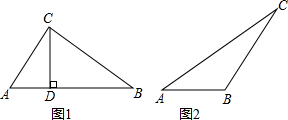
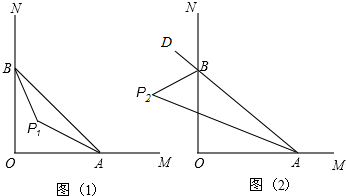
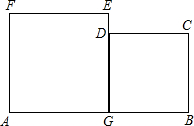 如图所示,这是一块工厂的下脚料铁板,其中AGEF和BCDG都是正方形.某个体水箱加工生产户经过计算得知,这块铁板的面积恰好等于他加工水箱所需的正方形铁板的面积(切割,焊接过程中的面积不变),他思考了一会,决定购买这块下脚料用于焊接冰箱.请你利用所学的知识帮助他设计一种最简便的切割,焊接方法,并证明你的设计方案.
如图所示,这是一块工厂的下脚料铁板,其中AGEF和BCDG都是正方形.某个体水箱加工生产户经过计算得知,这块铁板的面积恰好等于他加工水箱所需的正方形铁板的面积(切割,焊接过程中的面积不变),他思考了一会,决定购买这块下脚料用于焊接冰箱.请你利用所学的知识帮助他设计一种最简便的切割,焊接方法,并证明你的设计方案.