题目内容
三角形中的计算:
(1)如图所示,在△ABC中,∠ACB=90°,CD⊥AB于D,∠B=30°,AB=4
,求CD的长.
(2)已知,如图,△ABC中,∠A=30°,∠B=135°,AC=10,求AB及BC的长.
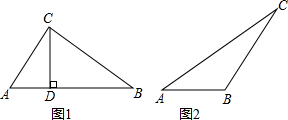
(1)如图所示,在△ABC中,∠ACB=90°,CD⊥AB于D,∠B=30°,AB=4
| 3 |
(2)已知,如图,△ABC中,∠A=30°,∠B=135°,AC=10,求AB及BC的长.

考点:解直角三角形
专题:
分析:(1)先在Rt△ABC中利用30°角所对的直角边等于斜边的一半得出AC=
AB=2
,再求出∠A=60°,然后解Rt△ACD,即可求出CD的长;
(2)过点C作CD⊥AB,交AB延长线于点D.解Rt△ACD得出CD=
AC=5,AD=5
,再证明△BCD是等腰直角三角形,于是BC=
CD=5
,BD=CD=5,那么AB=AD-BD=5
-5.
| 1 |
| 2 |
| 3 |
(2)过点C作CD⊥AB,交AB延长线于点D.解Rt△ACD得出CD=
| 1 |
| 2 |
| 3 |
| 2 |
| 2 |
| 3 |
解答:解:(1)如图1,在Rt△ABC中,∵∠ACB=90°,∠B=30°,AB=4
,
∴AC=
AB=2
,∠A=90°-∠B=60°.
在Rt△ACD中,∵∠ADC=90°,∠A=60°,
∴CD=AC•sin∠A=2
×
=3;
 (2)如图2,过点C作CD⊥AB,交AB延长线于点D.
(2)如图2,过点C作CD⊥AB,交AB延长线于点D.
在Rt△ACD中,∵∠ADC=90°,∠A=30°,AC=10,
∴CD=
AC=5,AD=AC•cos∠A=10×
=5
.
∵∠BDC=90°,∠CBD=180°-∠ABC=180°-135°=45°,
∴∠BCD=∠CBD=45°,
∴△BCD是等腰直角三角形,
∴BC=
CD=5
,BD=CD=5,
∴AB=AD-BD=5
-5.
| 3 |
∴AC=
| 1 |
| 2 |
| 3 |
在Rt△ACD中,∵∠ADC=90°,∠A=60°,
∴CD=AC•sin∠A=2
| 3 |
| ||
| 2 |
 (2)如图2,过点C作CD⊥AB,交AB延长线于点D.
(2)如图2,过点C作CD⊥AB,交AB延长线于点D.在Rt△ACD中,∵∠ADC=90°,∠A=30°,AC=10,
∴CD=
| 1 |
| 2 |
| ||
| 2 |
| 3 |
∵∠BDC=90°,∠CBD=180°-∠ABC=180°-135°=45°,
∴∠BCD=∠CBD=45°,
∴△BCD是等腰直角三角形,
∴BC=
| 2 |
| 2 |
∴AB=AD-BD=5
| 3 |
点评:本题考查了解直角三角形,等腰直角三角形的判定与性质,难度适中.准确作出辅助线,构造直角三角形是解决问题(2)的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若
-
=
,则
+
=( )
| 1 |
| a |
| 1 |
| b |
| 1 |
| a-b |
| b |
| a |
| a |
| b |
| A、1 | B、-1 | C、2 | D、-2 |
 如图,把⊙O1向右平移8个单位长度得到⊙O2,两圆相交于A、B,且O1 A、O2 A分别与⊙O2、⊙O1相切,切点均为A点,则图中阴影部分的面积为
如图,把⊙O1向右平移8个单位长度得到⊙O2,两圆相交于A、B,且O1 A、O2 A分别与⊙O2、⊙O1相切,切点均为A点,则图中阴影部分的面积为 公路同侧有A、B两个村庄,相距
公路同侧有A、B两个村庄,相距 在平行四边形ABCD中,点E、F在对角线AC上,且AE=CF,求证:∠EDF=∠EBF(用两种不同的方法证明)
在平行四边形ABCD中,点E、F在对角线AC上,且AE=CF,求证:∠EDF=∠EBF(用两种不同的方法证明)