Question

3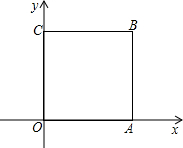．如图所示，正方形OABC的顶点为O（0，0），A（1，0），B（1，1），C（0，1）．
（1）判断直线y=-2x+$\frac{1}{3}$与正方形OABC是否有交点，并求交点坐标．
（2）将直线y=-2x+$\frac{1}{3}$进行平移，平移后恰好能把正方形OABC分为面积相等的两部分，请求出平移后的直线解析式．

Answer 1

分析 （1）根据四边形OABC为正方形，判断出直线$y=-2x+\frac{1}{3}$与正方形OABC有交点即可；
（2）直线平移后将正方形面积平分，即直线过正方形中心，设平移后直线解析式为y=-2x+b，把D坐标代入求出b的值，即可确定出平移后的直线解析式．

解答 解：（1）∵直线$y=-2x+\frac{1}{3}$与y轴交于点E（0，$\frac{1}{3}$），与x轴交于点F（$\frac{1}{6}$，0），
∴交点E在边OC上，交点F在边OA上，
∴直线$y=-2x+\frac{1}{3}$与正方形OABC有交点．                 
（2）连接AC、BO，交于点M，则点M的坐标为（$\frac{1}{2}$，$\frac{1}{2}$），
由题意知：平移后的直线经过点M（$\frac{1}{2}$，$\frac{1}{2}$），
设平移后的直线解析式为y=-2x+b，
则 将M（$\frac{1}{2}$，$\frac{1}{2}$）代入求得：$b=\frac{3}{2}$，
∴所求平移后的直线解析式为$y=-2x+\frac{3}{2}$．

点评 此题属于一次函数综合题，涉及的知识有：正方形的性质，坐标与图形性质，平移的性质，待定系数法确定一次函数解析式，熟练掌握性质是解本题的关键．