题目内容
12.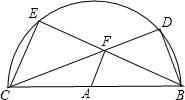 BC是半圆⊙A的直径,点D,E是圆上两点,并且∠DAE是直角,点F是弦CD、BE的交点.
BC是半圆⊙A的直径,点D,E是圆上两点,并且∠DAE是直角,点F是弦CD、BE的交点.(1)△EFC是什么三角形?
(2)如果AF∥CE,求DC:DB的值.
分析 (1)由BC是半圆⊙A的直径,得到∠CEF=∠BDF=90°,根据圆周角定理得到∠ECF=∠DBF=45°,即可得到结论;
(2)根据平行线的性质得到∠AFB=90°,根据三角形的中位线的性质得到EF=BF,根据勾股定理得到CF=$\sqrt{2}$BF,DF=DB=$\frac{\sqrt{2}}{2}$BF,即可得到结论.
解答 解:(1)△EFC是等腰直角三角形,
理由:∵BC是半圆⊙A的直径,
∴∠CEF=∠BDF=90°,
∵∠EAC=90°,
∴∠ECF=∠DBF=45°,
∴∠EFC=∠DFB=45°,
∴△EFC是等腰直角三角形;
(2)∵AF∥CE,
∴∠AFB=90°,
∵AC=BC,
∴EF=BF,
∴CF=$\sqrt{2}$BF,
∵△DFB是等腰直角三角形,
∴DF=DB=$\frac{\sqrt{2}}{2}$BF,
∴CD=CF+DF=$\frac{3\sqrt{2}}{2}$,
∴DC:DB=3.
点评 本题考查了等腰直角三角形的判定和性质,三角形的中位线的性质,平行线的性质,圆周角定理,根据圆周角定理得到∠ECF=∠DBF=45°是解题的关键.

练习册系列答案
相关题目
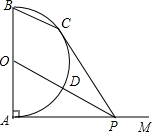 如图,AB是半圆O的直径,射线AM⊥AB,点P在AM上,连接OP交半圆O于点D,PC切半圆O于点C,连接BC.
如图,AB是半圆O的直径,射线AM⊥AB,点P在AM上,连接OP交半圆O于点D,PC切半圆O于点C,连接BC. 一块三角形纸板ABC,∠ACB=90°,AC=3,AB=5,把它置于平面直角坐标系中,AC∥y轴,BC∥x轴,顶点A,B恰好都在反比例函数y=$\frac{k}{x}$的图象上,AC,BC的延长线分别交x轴、y轴于D,E两点,设点C的坐标为(m,n).
一块三角形纸板ABC,∠ACB=90°,AC=3,AB=5,把它置于平面直角坐标系中,AC∥y轴,BC∥x轴,顶点A,B恰好都在反比例函数y=$\frac{k}{x}$的图象上,AC,BC的延长线分别交x轴、y轴于D,E两点,设点C的坐标为(m,n).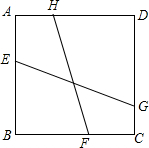 如图,正方形ABCD中,点E、F、G、H分别是在边AB、BC、CD、DA上,且EG与FH的夹角为45°,若正方形ABCD的边长是1.FH=$\frac{\sqrt{5}}{2}$,则EG的长度是$\frac{\sqrt{10}}{3}$.
如图,正方形ABCD中,点E、F、G、H分别是在边AB、BC、CD、DA上,且EG与FH的夹角为45°,若正方形ABCD的边长是1.FH=$\frac{\sqrt{5}}{2}$,则EG的长度是$\frac{\sqrt{10}}{3}$. 如图,点A,B,C,D为⊙O上的四个点,$\widehat{BC}$=$\widehat{CD}$,AC交BD于点E,CE=4,CD=6.
如图,点A,B,C,D为⊙O上的四个点,$\widehat{BC}$=$\widehat{CD}$,AC交BD于点E,CE=4,CD=6. △ABC中,AD平分∠BAC交BC于D,CH⊥AD于H.
△ABC中,AD平分∠BAC交BC于D,CH⊥AD于H.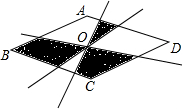 如图,四边形ABCD是菱形,点O是对角线的交点,三条直线都经过点O,图中阴影面积为24cm2,其中一对对角线长为6cm,则另一条对角线长为16cm.
如图,四边形ABCD是菱形,点O是对角线的交点,三条直线都经过点O,图中阴影面积为24cm2,其中一对对角线长为6cm,则另一条对角线长为16cm.