题目内容
17. △ABC中,AD平分∠BAC交BC于D,CH⊥AD于H.
△ABC中,AD平分∠BAC交BC于D,CH⊥AD于H.(1)求证:$\frac{AB}{AC}=\frac{BD}{DC}$;
(2)若AB=3,AC=5,BC=7,
①求BD的长;
②求H到BC中点M的距离.
分析 (1)如图1,过B作BN∥AC交AD的延长线于N,得到∠N=∠CAD,由AD平分∠BAC交BC于D,得到∠BAD=∠CAD,等量代换得到∠BAD=∠N,由等腰三角形的判定得到AB=BN,根据相似三角形的性质即可得到结论;
(2)①由$\frac{AB}{AC}=\frac{BD}{DC}$,代入数据即可得到结论;
②如图2,延长AB,CH交于E,连接HM,推出△AEH≌△ACH,根据全等三角形的性质得到AE=AC,EH=CH,根据三角形的中位线即可得到结论.
解答 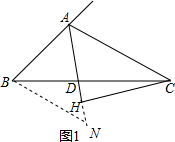 (1)证明:如图1,过B作BN∥AC交AD的延长线于N,
(1)证明:如图1,过B作BN∥AC交AD的延长线于N,
∴∠N=∠CAD,
∵AD平分∠BAC交BC于D,
∴∠BAD=∠CAD,
∴∠BAD=∠N,
∴AB=BN,
∵AC∥BN,
∴△BDN∽△ADC,
∴$\frac{BN}{AC}=\frac{BD}{CD}$,
$\frac{(\;\;\;\;)}{(\;\;\;\;)}$$\frac{AB}{AC}=\frac{BD}{CD}$;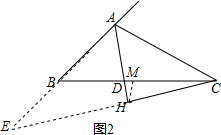
(2)解:①∵$\frac{AB}{AC}=\frac{BD}{DC}$,AB=3,AC=5,BC=7,
∴$\frac{3}{5}=\frac{BD}{7-BD}$,
∴BD=$\frac{21}{8}$;
②如图2,延长AB,CH交于E,连接HM,
∵CH⊥AD于H,
∴∠AHE=∠AHC=90°,
在△AEH于△ACH中,
$\left\{\begin{array}{l}{∠EAH=∠CAH}\\{AH=AH}\\{∠AHE=∠AHC}\end{array}\right.$,
∴△AEH≌△ACH,
∴AE=AC,EH=CH,
∴BE=AC-AB=2,
∵BM=CM,
∴HM=$\frac{1}{2}$BE=1.
点评 本题考查了全等三角形的判定和性质,相似三角形的判定和性质,三角形的中位线的性质,掌握的作出辅助线是解题的关键.

 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{5}$ |
| A. | 110°,70° | B. | 105°,75° | C. | 100°,70° | D. | 110°,80° |
| A. | 238×103 | B. | 2.38×105 | C. | 23.8×104 | D. | 0.238×106 |
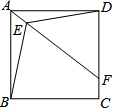 如图,E是正方形ABCD内一点,E到点A、D、B的距离EA、ED、EB分别为1、3$\sqrt{2}$、2$\sqrt{5}$,延长AE交CD于点F,则四边形BCFE的面积为$\frac{109}{8}$.
如图,E是正方形ABCD内一点,E到点A、D、B的距离EA、ED、EB分别为1、3$\sqrt{2}$、2$\sqrt{5}$,延长AE交CD于点F,则四边形BCFE的面积为$\frac{109}{8}$.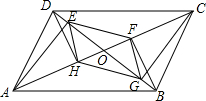 如图所示,平行四边形ABCD中,对角线AC、BD交于点O,AE⊥BD于点E,BF⊥AC于点F,CG⊥BD于点G,DH⊥AC于点H,求证:四边形EFGH是平行四边形.
如图所示,平行四边形ABCD中,对角线AC、BD交于点O,AE⊥BD于点E,BF⊥AC于点F,CG⊥BD于点G,DH⊥AC于点H,求证:四边形EFGH是平行四边形.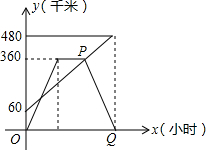 甲、乙两车分别从相距480km的A、B两地相向而行,乙车比甲车先出发1小时,并以各自的速度匀速行驶,途径C地,甲车到达C地停留1小时,因有事按原路原速返回A地.乙车从B地直达A地,两车同时到达A地.甲、乙两车距各自出发地的路程y(千米)与甲车出发所用的时间x(小时)的关系如图:
甲、乙两车分别从相距480km的A、B两地相向而行,乙车比甲车先出发1小时,并以各自的速度匀速行驶,途径C地,甲车到达C地停留1小时,因有事按原路原速返回A地.乙车从B地直达A地,两车同时到达A地.甲、乙两车距各自出发地的路程y(千米)与甲车出发所用的时间x(小时)的关系如图: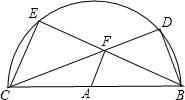 BC是半圆⊙A的直径,点D,E是圆上两点,并且∠DAE是直角,点F是弦CD、BE的交点.
BC是半圆⊙A的直径,点D,E是圆上两点,并且∠DAE是直角,点F是弦CD、BE的交点.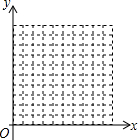 在平面直角坐标系中,设坐标轴的单位长度为1cm,整数点P从原点O出发,速度为1cm/s,且点P只能向上或向右运动,如点p从O点出发1秒时,点p的坐标为(0,1)(1,0),整数点个数为2个;点p从O点出发2秒时,点p的坐标为(0,2)(2,0),(1,1),整数点个数为3个…,当P点从点O出发10秒时,可得到整数点有11个;当P点从点O出发15秒时,可得到整数点(10,5).
在平面直角坐标系中,设坐标轴的单位长度为1cm,整数点P从原点O出发,速度为1cm/s,且点P只能向上或向右运动,如点p从O点出发1秒时,点p的坐标为(0,1)(1,0),整数点个数为2个;点p从O点出发2秒时,点p的坐标为(0,2)(2,0),(1,1),整数点个数为3个…,当P点从点O出发10秒时,可得到整数点有11个;当P点从点O出发15秒时,可得到整数点(10,5).