题目内容
17.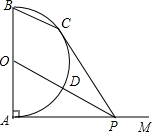 如图,AB是半圆O的直径,射线AM⊥AB,点P在AM上,连接OP交半圆O于点D,PC切半圆O于点C,连接BC.
如图,AB是半圆O的直径,射线AM⊥AB,点P在AM上,连接OP交半圆O于点D,PC切半圆O于点C,连接BC.(1)求证:BC∥OP;
(2)若半圆O的半径等于2,填空:
①当AP=2时,四边形OAPC是正方形;
②当AP=2$\sqrt{3}$时,四边形BODC是菱形.
分析 (1)根据切线的性质,可以得到OP⊥AC,由AB是圆O的直径,可以得到AC⊥BC,从而可以得到BC∥OP;
(2)①若四边形OAPC是正方形,根据正方形的性质可以得到AP的长;
②若四边形BODC是菱形,根据菱形的性质,通过变形,可以得到AP的长.
解答 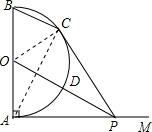 (1)证明:连接OC,AC,如右图所示,
(1)证明:连接OC,AC,如右图所示,
∵AB是直径,AM⊥AB,
∴BC⊥AC,AP是圆的切线,
∵PC切半圆O于点C,
∴PA=PC,
又∵OA=OC,
∴OP⊥AC,
∴BC∥OP;
(2)①若四边形OAPC是正方形,则OA=AP,
∵OA=2,
∴AP=2.
故答案为:2;
②若四边形BODC是菱形,则CB=BO=OD=DC,
∵AB=2OB,∠ACB=90°,
∴AB=2BC,
∴∠BAC=30°,∠ABC=60°,
∵BC∥OP,
∴∠AOP=∠ABC=60°,
又∵∠OAP=90°,OA=2,
∴∠OPA=30°,
∴OP=4,
∴AP=$\sqrt{O{P}^{2}-O{A}^{2}}=\sqrt{{4}^{2}-{2}^{2}}=2\sqrt{3}$,
故答案为:2$\sqrt{3}$.
点评 本题考查圆的综合题,解题的关键是明确题意,作出合适的辅助线,找出所求问题需要的条件,利用数形结合的思想解答问题.

练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
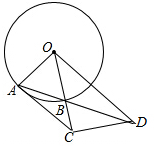 已知⊙O的半径OA=3,B为⊙O上一点,延长OB,在OB延长线上截取一点C,使得BC=2,CD垂直于BC交AB延长线于点D,连接AC,若AC=CD,则AB=$\frac{6\sqrt{5}}{5}$.
已知⊙O的半径OA=3,B为⊙O上一点,延长OB,在OB延长线上截取一点C,使得BC=2,CD垂直于BC交AB延长线于点D,连接AC,若AC=CD,则AB=$\frac{6\sqrt{5}}{5}$.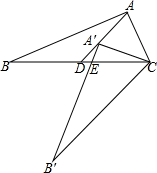 如图,Rt△ABC中,∠BAC=90°,将△ABC绕点C逆时针旋转,旋转后的图形是△A′B′C,点A的对应点A′落在中线AD上,且点A′是△ABC的重心,A′B′与BC相交于点E,那么BE:CE=4:3.
如图,Rt△ABC中,∠BAC=90°,将△ABC绕点C逆时针旋转,旋转后的图形是△A′B′C,点A的对应点A′落在中线AD上,且点A′是△ABC的重心,A′B′与BC相交于点E,那么BE:CE=4:3.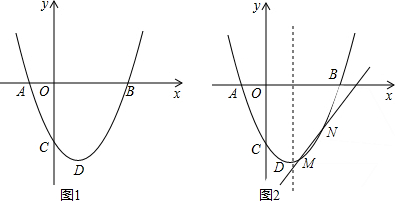
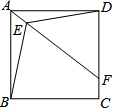 如图,E是正方形ABCD内一点,E到点A、D、B的距离EA、ED、EB分别为1、3$\sqrt{2}$、2$\sqrt{5}$,延长AE交CD于点F,则四边形BCFE的面积为$\frac{109}{8}$.
如图,E是正方形ABCD内一点,E到点A、D、B的距离EA、ED、EB分别为1、3$\sqrt{2}$、2$\sqrt{5}$,延长AE交CD于点F,则四边形BCFE的面积为$\frac{109}{8}$.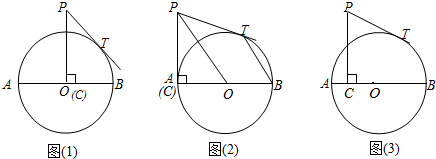
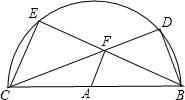 BC是半圆⊙A的直径,点D,E是圆上两点,并且∠DAE是直角,点F是弦CD、BE的交点.
BC是半圆⊙A的直径,点D,E是圆上两点,并且∠DAE是直角,点F是弦CD、BE的交点.