题目内容
13.解方程:①$\frac{x-3}{x-2}$+1=$\frac{3}{2-x}$;
②$\frac{x}{x-2}$-$\frac{1}{{x}^{2}-4}$=1.
分析 两分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:①去分母得:x-3+x-2=-3,
解得:x=1,
经检验x=1是分式方程的解;
②去分母得:x2+2x-1=x2-4,
解得:x=-1.5,
经检验x=-1.5是分式方程的解.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
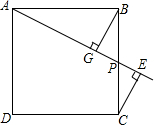 P是边长为4的正方形ABCD的边BC上任一点,过B作BG⊥AP于G,过C作CE⊥AP于E,连BE.
P是边长为4的正方形ABCD的边BC上任一点,过B作BG⊥AP于G,过C作CE⊥AP于E,连BE.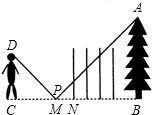 王明同学为了测量河对岸树AB的高度.他在河岸边放一面平面镜MN,他站在C处通过平面镜看到树的顶端A.如图,然后他量得B、P间的距离是56米,C、P间距离是12米,他的身高是1.74米.请你帮他计算出树AB的高度.
王明同学为了测量河对岸树AB的高度.他在河岸边放一面平面镜MN,他站在C处通过平面镜看到树的顶端A.如图,然后他量得B、P间的距离是56米,C、P间距离是12米,他的身高是1.74米.请你帮他计算出树AB的高度.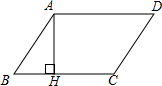 如图,在?ABCD中,AB=8cm,BC=10cm,∠B=60°.
如图,在?ABCD中,AB=8cm,BC=10cm,∠B=60°. 如图,直角三角形ABC的两条直角边AB和BC分别长4厘米和3厘米,现在以斜边AC为轴旋转一周.求所形成的立体图形的体积.
如图,直角三角形ABC的两条直角边AB和BC分别长4厘米和3厘米,现在以斜边AC为轴旋转一周.求所形成的立体图形的体积.