题目内容
18.已知:字母a、b满足$\sqrt{a-1}+\sqrt{b-2}$=0,求$\frac{1}{ab}$$+\frac{1}{(a+1)(b+1)}$$+\frac{1}{(a+2)(b+2)}$+…+$\frac{1}{(a+2014)(b+2014)}$的值.分析 由二次根式的非负性得出a=1,b=2,代入原式根据$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$拆分原式即可求值.
解答 解:∵$\sqrt{a-1}+\sqrt{b-2}$=0,
∴a=1,b=2,
则原式=$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{2015×2016}$
=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{2015}$-$\frac{1}{2016}$
=1-$\frac{1}{2016}$
=$\frac{2015}{2016}$.
点评 本题主要考查二次根式的非负性及分式的化简求值能力,将原式根据$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$拆分计算是解题的关键.

练习册系列答案
相关题目
6.下列图形(如图所示)经过折叠不能围成正方体的是( )
| A. |  | B. |  | C. |  | D. |  |
 是方程N的一个根;
是方程N的一个根;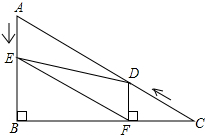 如图,在Rt△ABC中,∠B=90°,AC=10,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
如图,在Rt△ABC中,∠B=90°,AC=10,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.