题目内容
6.求(1-$\frac{1}{{2}^{2}}$)(1-$\frac{1}{{3}^{2}}$)(1-$\frac{1}{{4}^{2}}$)…(1-$\frac{1}{{9}^{2}}$)的值.分析 原式利用平方差公式化简,结合后相乘即可得到结果.
解答 解:原式=(1+$\frac{1}{2}$)(1-$\frac{1}{2}$)(1+$\frac{1}{3}$)(1-$\frac{1}{3}$)…(1+$\frac{1}{9}$)(1-$\frac{1}{9}$)
=(1+$\frac{1}{2}$)(1+$\frac{1}{3}$)…(1+$\frac{1}{9}$)(1-$\frac{1}{2}$)(1-$\frac{1}{3}$)…(1-$\frac{1}{9}$)
=$\frac{3}{2}$×$\frac{4}{3}$×…×$\frac{10}{9}$×$\frac{1}{2}$×$\frac{2}{3}$×…×$\frac{8}{9}$
=5×$\frac{1}{9}$
=$\frac{5}{9}$.
点评 此题考查了平方差公式,熟练掌握平方差公式是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.当$\frac{2a-5}{{\sqrt{a-3}}}$有意义时,a的取值范围是( )
| A. | a≥3 | B. | a>3 | C. | a≠3 | D. | a≠-3 |
1.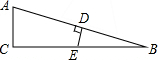 如图,在△ABC中,∠C=90°,∠B=15°,AB的垂直平分线交AB于D,交BC于E,若BE=8cm,则AC的长为( )
如图,在△ABC中,∠C=90°,∠B=15°,AB的垂直平分线交AB于D,交BC于E,若BE=8cm,则AC的长为( )
 如图,在△ABC中,∠C=90°,∠B=15°,AB的垂直平分线交AB于D,交BC于E,若BE=8cm,则AC的长为( )
如图,在△ABC中,∠C=90°,∠B=15°,AB的垂直平分线交AB于D,交BC于E,若BE=8cm,则AC的长为( )| A. | 4cm | B. | 5cm | C. | 6cm | D. | 8cm |
16.等腰三角形的周长为9,一边长为4,则腰长为( )
| A. | 5 | B. | 4 | C. | 2.5 | D. | 2.5或4 |
 已知有理数a、b 在数轴上的位置如图所示.
已知有理数a、b 在数轴上的位置如图所示. 如图,平面上有A,B,C,D四个村庄,为了丰富群众和生活,政府准备投资修建一个文化活动中心H,使它到四个村庄的距离之和最小,你认为文化活动中心应建在AC、BD连线的交点处,理由是两点之间线段最短.
如图,平面上有A,B,C,D四个村庄,为了丰富群众和生活,政府准备投资修建一个文化活动中心H,使它到四个村庄的距离之和最小,你认为文化活动中心应建在AC、BD连线的交点处,理由是两点之间线段最短. 如图,在四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=10,DA=5$\sqrt{5}$,则cos∠DBC的值为$\frac{5\sqrt{41}}{41}$.
如图,在四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=10,DA=5$\sqrt{5}$,则cos∠DBC的值为$\frac{5\sqrt{41}}{41}$.