题目内容
1．
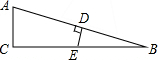如图，在△ABC中，∠C=90°，∠B=15°，AB的垂直平分线交AB于D，交BC于E，若BE=8cm，则AC的长为（ ）| A． | 4cm | B． | 5cm | C． | 6cm | D． | 8cm |
分析 由线段AB的垂直平分线DE交BC于D，交AB于E，E为垂足，根据线段垂直平分线的性质，可求得DB=AD，继而求得∠DAE=∠B=15°，则可求得∠ADC的度数，然后由含30°的直角三角形的性质，求得答案．
解答 解：∵DE是线段AB的垂直平分线，
∴AD=DB=8cm，
∴∠DAE=∠B=15°，
∴∠ADC=∠DAE+∠B=30°，
∵∠ACB=90°，
∴AC=$\frac{1}{2}$AD=4cm．
故选A．
点评 此题考查了线段垂直平分线的性质以及含30°的直角三角形的性质．注意求得∠ADC=30°是关键．
练习册系列答案
相关题目
11．
如图，已知直线y=-$\frac{3}{4}$x+3与x轴、y轴分别交于A、B两点，点C（0，n）是y轴正半轴上一点．把坐标平面沿直线AC折叠，使点B刚好落在x轴上，则n的值是（ ）
如图，已知直线y=-$\frac{3}{4}$x+3与x轴、y轴分别交于A、B两点，点C（0，n）是y轴正半轴上一点．把坐标平面沿直线AC折叠，使点B刚好落在x轴上，则n的值是（ ）| A． | $\frac{3}{4}$ | B． | 1 | C． | $\frac{4}{3}$ | D． | 1.5 |
9．抛物线y=x2-1，当y＞0时x的范围是（ ）
| A． | x＞1 | B． | x＜-1 | C． | 0＜x＜1 | D． | x＜-1或x＞1 |
16．到三角形三个顶点距离相等的点是三角形的（ ）
| A． | 内心 | B． | 外心 | C． | 重心 | D． | 垂心 |
13．下列图案中，既是轴对称图形，又是中心对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |