题目内容
5.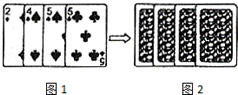 四张扑克牌的牌面如图1,将扑克牌洗匀后,如图2背面朝上放置在桌面上,小明和小亮设计了A、B两种游戏方案:
四张扑克牌的牌面如图1,将扑克牌洗匀后,如图2背面朝上放置在桌面上,小明和小亮设计了A、B两种游戏方案:方案A:随机抽一张扑克牌,牌面数字为5时小明获胜;否则小亮获胜.
方案B:随机同时抽取两张扑克牌,两张牌面数字之和为偶数时,小明获胜;否则小亮获胜.
请你帮小亮选择其中一种方案,使他获胜的可能性较大,并说明理由.
分析 由四张扑克牌的牌面是5的有2种情况,不是5的也有2种情况,可求得方案A中,小亮获胜的概率;
首先根据题意画出树状图,然后由树状图求得所有等可能的结果与小亮获胜的情况,再利用概率公式即可求得答案;比较其大小,即可求得答案.
解答 解:小亮选择B方案,使他获胜的可能性较大.理由如下:
方案A:∵四张扑克牌的牌面是5的有2种情况,不是5的也有2种情况,
∴P(小亮获胜)=$\frac{2}{4}$=$\frac{1}{2}$;
方案B:画树状图得:
∵ 共有12种等可能的结果,两张牌面数字之和为偶数的有4种情况,不是偶数的有8种情况,
共有12种等可能的结果,两张牌面数字之和为偶数的有4种情况,不是偶数的有8种情况,
∴P(小亮获胜)=$\frac{8}{12}$=$\frac{2}{3}$;
∴小亮选择B方案,使他获胜的可能性较大.
点评 此题主要考查了游戏公平性,列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合于两步或两步以上的完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
16.某校举办初中生演讲比赛,每班派一名学生参赛,现某班有A,B,C三名学生竞选,他们的笔试成绩和口试成绩分别用两种方式进行了统计,如表和图1:

(1)请将表和图1中的空缺部分补充完整.
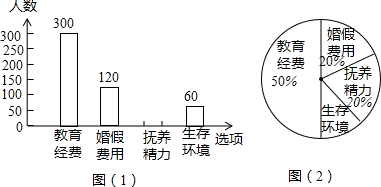
(2)竞选的最后一个程序是由本年级段的300名学生代表进行投票,每票计1分,三名候选人的得票情况如图2(没有弃权票,每名学生只能推荐一人),若将笔试、口试、得票三项测试得分按3:4:3的比例确定最后成绩,请计算这三名学生的最后成绩,并根据最后成绩判断谁能当选.
| 学生 | A | B | C |
| 笔试成绩(单位:分) | 85 | 95 | 90 |
| 口试成绩(单位:分) | 90 | 80 | 85 |

(1)请将表和图1中的空缺部分补充完整.
(2)竞选的最后一个程序是由本年级段的300名学生代表进行投票,每票计1分,三名候选人的得票情况如图2(没有弃权票,每名学生只能推荐一人),若将笔试、口试、得票三项测试得分按3:4:3的比例确定最后成绩,请计算这三名学生的最后成绩,并根据最后成绩判断谁能当选.
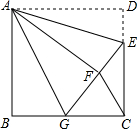 如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:
如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论: