题目内容
16.某校举办初中生演讲比赛,每班派一名学生参赛,现某班有A,B,C三名学生竞选,他们的笔试成绩和口试成绩分别用两种方式进行了统计,如表和图1:| 学生 | A | B | C |
| 笔试成绩(单位:分) | 85 | 95 | 90 |
| 口试成绩(单位:分) | 90 | 80 | 85 |

(1)请将表和图1中的空缺部分补充完整.
(2)竞选的最后一个程序是由本年级段的300名学生代表进行投票,每票计1分,三名候选人的得票情况如图2(没有弃权票,每名学生只能推荐一人),若将笔试、口试、得票三项测试得分按3:4:3的比例确定最后成绩,请计算这三名学生的最后成绩,并根据最后成绩判断谁能当选.
分析 (1)根据条形统计图找出A的口试成绩,填写表格即可;找出C的笔试成绩,补全条形统计图即可;
(2)由300分别乘以扇形统计图中各学生的百分数即可得到各自的得分,再根据加权平均数的计算方法计算可得.
解答 解:(1)由条形统计图得:A同学的口试成绩为90;补充直方图,如图所示:
| A | B | C | |
| 笔试 | 85 | 95 | 90 |
| 口试 | 90 | 80 | 85 |
∴$\overline{{x}_{A}}$=$\frac{85×3+90×4+105×3}{10}$=93,$\overline{{x}_{B}}$=$\frac{95×3+80×4+120×3}{10}$=96.5,$\overline{{x}_{C}}$=$\frac{90×3+85×4+75×3}{10}$=83.5,
∵$\overline{{x}_{B}}$>$\overline{{x}_{A}}$>$\overline{{x}_{C}}$,
∴B学生能当选.
点评 此题考查了条形统计图、扇形统计图及加权平均数的计算,能正确识别表格与统计图是解本题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
8. 二次函数y=-x2+mx的图象如图,对称轴为直线x=2,若关于x的一元二次方程-x2+mx-t=0(t为实数)在1<x<5的范围内有解,则t的取值范围是( )
二次函数y=-x2+mx的图象如图,对称轴为直线x=2,若关于x的一元二次方程-x2+mx-t=0(t为实数)在1<x<5的范围内有解,则t的取值范围是( )
 二次函数y=-x2+mx的图象如图,对称轴为直线x=2,若关于x的一元二次方程-x2+mx-t=0(t为实数)在1<x<5的范围内有解,则t的取值范围是( )
二次函数y=-x2+mx的图象如图,对称轴为直线x=2,若关于x的一元二次方程-x2+mx-t=0(t为实数)在1<x<5的范围内有解,则t的取值范围是( )| A. | t>-5 | B. | -5<t<3 | C. | 3<t≤4 | D. | -5<t≤4 |
6.下列能判定△ABC为等腰三角形的是( )
| A. | AB=AC=3,BC=6 | B. | ∠A=40°、∠B=70° | ||
| C. | AB=3、BC=8,周长为16 | D. | ∠A=40°、∠B=50° |
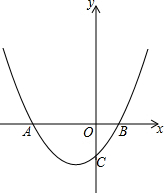 如图,在平面直角坐标系中,点O为坐标原点,抛物线y=ax2+6ax-4与x轴的负半轴相交于点A,与x轴的正半轴相交于点B,与y轴的负半轴相交于点C,且AB=10,一次函数y=x+b与抛物线相交于点E和点F(点E在点F左边),与抛物线的对称轴相交于点G.
如图,在平面直角坐标系中,点O为坐标原点,抛物线y=ax2+6ax-4与x轴的负半轴相交于点A,与x轴的正半轴相交于点B,与y轴的负半轴相交于点C,且AB=10,一次函数y=x+b与抛物线相交于点E和点F(点E在点F左边),与抛物线的对称轴相交于点G.
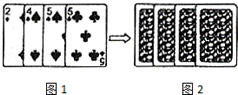 四张扑克牌的牌面如图1,将扑克牌洗匀后,如图2背面朝上放置在桌面上,小明和小亮设计了A、B两种游戏方案:
四张扑克牌的牌面如图1,将扑克牌洗匀后,如图2背面朝上放置在桌面上,小明和小亮设计了A、B两种游戏方案: