题目内容
16.先化简,再求值:$\frac{x}{{x}^{2}+2x}$-$\frac{{x}^{2}+2x+1}{x+2}$÷$\frac{{x}^{2}-1}{x-1}$,其中x=3.分析 先算除法,再算减法,最后把x的值代入进行计算即可.
解答 解:原式=$\frac{x}{x(x+2)}$-$\frac{(x+1)^{2}}{x+2}$•$\frac{x-1}{(x+1)(x-1)}$
=$\frac{x}{x(x+2)}$-$\frac{{(x+1)}^{2}}{x+2}$•$\frac{1}{x+1}$
=$\frac{1}{x+2}$-$\frac{x+1}{x+2}$
=$\frac{1-x-1}{x+2}$
=-$\frac{x}{x+2}$.
当x=3时,原式=-$\frac{3}{5}$.
点评 本题考查的是分式的化简求值,分式中的一些特殊求值题并非是一味的化简,代入,求值.许多问题还需运用到常见的数学思想,如化归思想(即转化)、整体思想等,了解这些数学解题思想对于解题技巧的丰富与提高有一定帮助.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
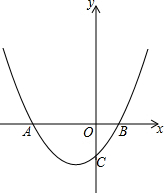 如图,在平面直角坐标系中,点O为坐标原点,抛物线y=ax2+6ax-4与x轴的负半轴相交于点A,与x轴的正半轴相交于点B,与y轴的负半轴相交于点C,且AB=10,一次函数y=x+b与抛物线相交于点E和点F(点E在点F左边),与抛物线的对称轴相交于点G.
如图,在平面直角坐标系中,点O为坐标原点,抛物线y=ax2+6ax-4与x轴的负半轴相交于点A,与x轴的正半轴相交于点B,与y轴的负半轴相交于点C,且AB=10,一次函数y=x+b与抛物线相交于点E和点F(点E在点F左边),与抛物线的对称轴相交于点G.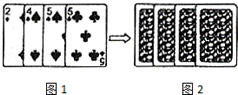 四张扑克牌的牌面如图1,将扑克牌洗匀后,如图2背面朝上放置在桌面上,小明和小亮设计了A、B两种游戏方案:
四张扑克牌的牌面如图1,将扑克牌洗匀后,如图2背面朝上放置在桌面上,小明和小亮设计了A、B两种游戏方案: