题目内容
6.解方程:(1)x-2=x(x-2)
(2)2x2-x-1=0(用配方法解方程)
(3)x2-4x-1=0 (用公式法解方程)
分析 (1)移项,分解因式,利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程来求解.
(2)首先将常数项移到等号的右侧,把二次项系数化为1,再将等号左右两边同时加上一次项系数一半的平方,即可将等号左边的代数式写成完全平方形式.
(3)观察方程为一般形式,找出此时二次项系数,一次项系数及常数项,计算出根的判别式,发现其结果大于0,故利用求根公式可得出方程的两个解.
解答 解:(1)x-2=x(x-2)
(x-2)-x(x-2)=0,
(x-2)(1-x)=0,
∴x-2=0,1-x=0,
∴x1=2,x2=1;
(2)2x2-x-1=0
x2-$\frac{1}{2}$x=$\frac{1}{2}$,
x2-$\frac{1}{2}$x+$\frac{1}{16}$=$\frac{1}{2}$+$\frac{1}{16}$,
(x-$\frac{1}{4}$)2=$\frac{9}{16}$,
∴x-$\frac{1}{4}$=±$\frac{3}{4}$,
∴x1=1,x2=-$\frac{1}{2}$;
(3)x2-4x-1=0,
∵a=1,b=-4,c=-1,b2-4ac=16+4=20,
∴x=$\frac{4±\sqrt{20}}{2×1}$=2±$\sqrt{5}$,
∴x1=2+$\sqrt{5}$,x2=2-$\sqrt{5}$.
点评 此题考查了解一元二次方程,熟练掌握因式分解法、配方法、公式法是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.一个球的内部挖去一个最大的正方体(正方体的八个顶点都在球的表面上),用一个平面去截这个几何体,其截面形状有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
16.计算2sin30°-sin245°+tan30°的结果是( )
| A. | $\frac{1}{2}$+3$\sqrt{3}$ | B. | $\frac{1}{2}$+$\frac{\sqrt{3}}{3}$ | C. | $\sqrt{3}$+$\sqrt{2}$ | D. | 1-$\sqrt{3}$+$\sqrt{2}$ |
 已知,如图?ABCD中,E为AD边上的一点,AE:ED=2:5,连结AC、BE交于点F,若AC=20cm,则AF=$\frac{40}{9}$,CF=$\frac{140}{9}$.
已知,如图?ABCD中,E为AD边上的一点,AE:ED=2:5,连结AC、BE交于点F,若AC=20cm,则AF=$\frac{40}{9}$,CF=$\frac{140}{9}$.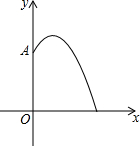 某地要建造一个圆形喷水池,在水池中央垂直于地面安装一个柱子OA,O恰为水面中心,安置在柱子顶端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下.在过OA的任一平面上,建立平面直角坐标系(如图),水流喷出的高度y(m)与水平距离x(m)之间的关系式是y=-x2+2x+$\frac{5}{4}$,则下列结论:
某地要建造一个圆形喷水池,在水池中央垂直于地面安装一个柱子OA,O恰为水面中心,安置在柱子顶端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下.在过OA的任一平面上,建立平面直角坐标系(如图),水流喷出的高度y(m)与水平距离x(m)之间的关系式是y=-x2+2x+$\frac{5}{4}$,则下列结论: