题目内容
 如图,在Rt△ABC中∠ABC=90°,以AB为直径作圆O交AC于E,连接E点和CB的中点D.
如图,在Rt△ABC中∠ABC=90°,以AB为直径作圆O交AC于E,连接E点和CB的中点D.(1)DE是圆O的切线吗?如果是请说明理由.
(2)若AE和AB的长度分别为一元二次方程x2-10x+24=0的两个根,求BC的长度?
考点:切线的判定,解一元二次方程-因式分解法
专题:计算题
分析:(1)连结OE、BE,如图,先根据圆周角定理得到∠AEB=90°,再利用直角三角形斜边上的中线性质得到DE=DB=DC,再利用等腰三角形的性质得∠1=∠2,∠3=∠4,则∠2+∠3=∠1+∠4=90°,即∠ODE=90°,然后根据切线的判定定理即可得到DE是⊙O的切线;
(2)先解方程得到AE=4,AB=6,再证明Rt△ABE∽Rt△ABC,则利用相似比可计算出AC=9,然后利用勾股定理计算BC的长.
(2)先解方程得到AE=4,AB=6,再证明Rt△ABE∽Rt△ABC,则利用相似比可计算出AC=9,然后利用勾股定理计算BC的长.
解答:解:(1)DE为圆O的切线.理由如下:
连结OE、BE,如图,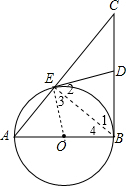
∵AB是⊙O的直径,
∴∠AEB=90°.
∴∠CEB=90°
又∵D为BC的中点,
∴DE=DB=DC,
∴∠1=∠2,
∵OE=OB,
∴∠3=∠4,
∵∠ABC=90°,
∴∠2+∠3=∠1+∠4=90°,即∠OED=90°,
∴OE⊥DE,
∴DE是⊙O的切线;
(2)解方程x2-10x+24=0得x1=4,x2=6,
∴AE=4,AB=6,
∵∠BAE=∠CAB,
∴Rt△ABE∽Rt△ABC,
∴
=
,即
=
,
∴AC=9,
在Rt△ABC中,∵AB=6,AC=9,
∴BC=
=3
.
连结OE、BE,如图,

∵AB是⊙O的直径,
∴∠AEB=90°.
∴∠CEB=90°
又∵D为BC的中点,
∴DE=DB=DC,
∴∠1=∠2,
∵OE=OB,
∴∠3=∠4,
∵∠ABC=90°,
∴∠2+∠3=∠1+∠4=90°,即∠OED=90°,
∴OE⊥DE,
∴DE是⊙O的切线;
(2)解方程x2-10x+24=0得x1=4,x2=6,
∴AE=4,AB=6,
∵∠BAE=∠CAB,
∴Rt△ABE∽Rt△ABC,
∴
| AE |
| AB |
| AB |
| AC |
| 4 |
| 6 |
| 6 |
| AC |
∴AC=9,
在Rt△ABC中,∵AB=6,AC=9,
∴BC=
| AC2-AB2 |
| 5 |
点评:本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了等腰三角形的性质和相似三角形的判定与性质.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
 如图,△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、F,连接BD交0F于点E.
如图,△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、F,连接BD交0F于点E. 如图,OA=OB,点A的坐标是(-2,0),OB与x轴正方向夹角为60°,请画出过A,O,B三点的圆,写出圆心的坐标是
如图,OA=OB,点A的坐标是(-2,0),OB与x轴正方向夹角为60°,请画出过A,O,B三点的圆,写出圆心的坐标是 已知,在Rt△ABC中,∠ABC=90°,D是AC的中点,⊙O经过A,D,B三点,CB的延长线交⊙O于点E,延长AC至F,使得CF=CD,连接EF
已知,在Rt△ABC中,∠ABC=90°,D是AC的中点,⊙O经过A,D,B三点,CB的延长线交⊙O于点E,延长AC至F,使得CF=CD,连接EF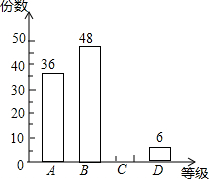 某校为了选拔省教委组织的以“爱我省会•让节能环保称为时尚”为主题的参赛作品,现在本校组织了一次“以爱我家乡•让节能环保成为时尚”的作品征集活动,现从所收集上来的作品中随机爱抽取了一部分,按A,B,C,D四个等级进行评选,并根据评选结果绘制了如图所示的条形统计图,已知等级C的作品的所抽取作品中占25%.
某校为了选拔省教委组织的以“爱我省会•让节能环保称为时尚”为主题的参赛作品,现在本校组织了一次“以爱我家乡•让节能环保成为时尚”的作品征集活动,现从所收集上来的作品中随机爱抽取了一部分,按A,B,C,D四个等级进行评选,并根据评选结果绘制了如图所示的条形统计图,已知等级C的作品的所抽取作品中占25%. 如图,△ABC中,AD是中线,AE是角平分线,CF垂直AE于点F,AB=5,AC=2,则FD的长是
如图,△ABC中,AD是中线,AE是角平分线,CF垂直AE于点F,AB=5,AC=2,则FD的长是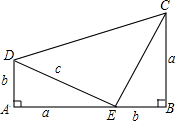 如图所示,△ADE≌△BEC,∠A=∠B=90°,A,D,B三点在一条直线上,借助这个图形,你能用面积法来验证勾股定理吗?
如图所示,△ADE≌△BEC,∠A=∠B=90°,A,D,B三点在一条直线上,借助这个图形,你能用面积法来验证勾股定理吗?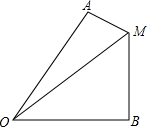 如图,已知∠AOB=60°,MA⊥OA于点A,MB⊥OB于点B,MA=2,MB=11,求OM的长.
如图,已知∠AOB=60°,MA⊥OA于点A,MB⊥OB于点B,MA=2,MB=11,求OM的长.