题目内容
10．
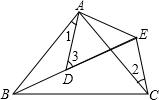如图所示，AB=AC，AD=AE，∠BAC=∠DAE，∠1=20°，∠2=35°，则∠3=55°．
分析 根据等式的性质得出∠BAD=∠CAE，再利用全等三角形的判定和性质解答即可．
解答 解：∵∠BAC=∠DAE，
∴∠BAC-∠DAC=∠DAE-∠DAC，
即∠BAD=∠CAE，
在△BAD与△CAE中，
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAE}\\{AD=AE}\end{array}\right.$，
∴△BAD≌△CAE（SAS），
∴∠ABD=∠2=35°，
∴∠3=∠1+∠ABD=35°+20°=55°．
故答案为：55°．
点评 此题考查全等三角形的判定和性质，关键是根据等式的性质得出∠BAD=∠CAE．
练习册系列答案
相关题目
作图题：在图中画出△ABC关于直线l的轴对称图形△A1B1C1．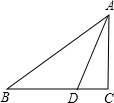
如图，△ABC中∠C=90°，点D在BC上，且DB=DA，tan∠DAC=$\frac{1}{2}$，则tanB=$\frac{\sqrt{5}-1}{2}$．
如图，⊙O是△ABC的外接圆，∠BOC=40°，则∠A的度数为20°．