题目内容
20.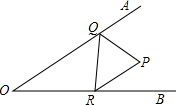 已知∠AOB=30°,在∠AOB的内部有一个定点P,OP=10,在∠AOB的两边OA、OB上分别有动点Q、R(不与点O重合),则△PQR周长的最小值是10.
已知∠AOB=30°,在∠AOB的内部有一个定点P,OP=10,在∠AOB的两边OA、OB上分别有动点Q、R(不与点O重合),则△PQR周长的最小值是10.
分析 根据轴对称图形的性质,作出P关于OA、OB的对称点M、N,连接MN,根据两点之间线段最短得到最小值线段,根据等边三角形的性质解答即可.
解答 解:分别作P关于OA、OB的对称点M、N.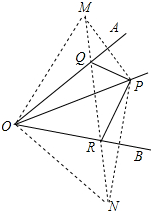
连接MN交OA、OB交于Q、R,则△PQR符合条件.
连接OM、ON,
由轴对称的性质可知,OM=ON=OP=10,
∠MON=∠MOP+∠NOP=2∠AOB=2×30°=60°,
则△MON为等边三角形,
∴MN=10,
∵QP=QM,RN=RP,
∴△PQR周长=MN=10,
故答案为:10.
点评 本题考查了轴对称-最短路径问题,根据轴对称的性质作出对称点是解题的关键,掌握线段垂直平分线的性质和等边三角形的性质的灵活运用.

练习册系列答案
相关题目
15.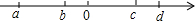 有理数a、b、c、d在数轴上的位置如图所示,下列结论中错误的是( )
有理数a、b、c、d在数轴上的位置如图所示,下列结论中错误的是( )
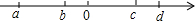 有理数a、b、c、d在数轴上的位置如图所示,下列结论中错误的是( )
有理数a、b、c、d在数轴上的位置如图所示,下列结论中错误的是( )| A. | a+b<0 | B. | c+d>0 | C. | |a+c|=a+c | D. | |b+d|=b+d |
5.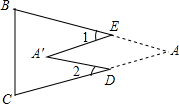 如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变.请试着找一找这个规律,你发现的规律是( )
如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变.请试着找一找这个规律,你发现的规律是( )
 如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变.请试着找一找这个规律,你发现的规律是( )
如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变.请试着找一找这个规律,你发现的规律是( )| A. | ∠A=∠1+∠2 | B. | 2∠A=∠1+∠2 | C. | 3∠A=2∠1+∠2 | D. | 3∠A=2(∠1+∠2) |
9.已知⊙O1和⊙O2相切,⊙O1的直径为9cm,⊙O2的直径为4cm,则O1O2的长是( )
| A. | 5cm或13cm | B. | 2.5cm | C. | 6.5cm | D. | 2.5cm或6.5cm |
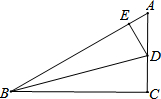
 如图,M、P分别是△ABC的边AB、BC上的点,在AC上求作一点N,使△PMN的周长最小,并说明你这样作的理由.
如图,M、P分别是△ABC的边AB、BC上的点,在AC上求作一点N,使△PMN的周长最小,并说明你这样作的理由.
 如图,在Rt△ABC中,∠C=90°,BD是∠ABC的平分线,DE⊥AB于点E.若DE=2cm,则DC的长度为2cm.
如图,在Rt△ABC中,∠C=90°,BD是∠ABC的平分线,DE⊥AB于点E.若DE=2cm,则DC的长度为2cm.