题目内容
13.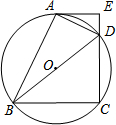 如图,四边形ABCD内接于⊙O,BD是⊙O的直径,过点A作AE⊥CD,交CD的延长线于点E,DA平分∠BDE.
如图,四边形ABCD内接于⊙O,BD是⊙O的直径,过点A作AE⊥CD,交CD的延长线于点E,DA平分∠BDE.(1)求证:AE是⊙O的切线;
(2)已知AE=8cm,CD=12cm,求⊙O的半径.
分析 (1)根据等边对等角得出∠ODA=∠OAD,进而得出∠OAD=∠EDA,证得EC∥OA,从而证得AE⊥OA,即可证得AE是⊙O的切线;
(2)过点O作OF⊥CD,垂足为点F.从而证得四边形AOFE是矩形,得出OF=AE=8cm,根据垂径定理得出DF=$\frac{1}{2}$CD=6cm,在Rt△ODF中,根据勾股定理即可求得⊙O的半径.
解答 (1)证明:连结OA.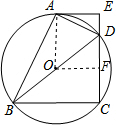
∵OA=OD,
∴∠ODA=∠OAD.
∵DA平分∠BDE,
∴∠ODA=∠EDA.
∴∠OAD=∠EDA,
∴EC∥OA.
∵AE⊥CD,
∴OA⊥AE.
∵点A在⊙O上,
∴AE是⊙O的切线.
(2)解:过点O作OF⊥CD,垂足为点F.
∵∠OAE=∠AED=∠OFD=90°,
∴四边形AOFE是矩形.
∴OF=AE=8cm.
又∵OF⊥CD,
∴DF=$\frac{1}{2}$CD=6cm.
在Rt△ODF中,OD=$\sqrt{O{F^2}+D{F^2}}$=10cm,
即⊙O的半径为10cm.
点评 本题考查了等腰三角形的性质,垂径定理,平行线的判定和性质,切线的判定和性质,勾股定理的应用等,熟练掌握性质定理是解题的关键.

练习册系列答案
相关题目
2.数据显示,2015年全国新建、改扩建校舍约为51 660 000平方米,全面改善贫困地区义务教育薄弱学校基本办学条件工作取得明显成果.将数据51 660 000用科学记数法表示应为( )
| A. | 5.166×107 | B. | 5.166×108 | C. | 51.66×106 | D. | 0.5166×108 |
 (1)解二元一次方程组$\left\{\begin{array}{l}{2x-y=4}\\{3x+y=1}\end{array}\right.$
(1)解二元一次方程组$\left\{\begin{array}{l}{2x-y=4}\\{3x+y=1}\end{array}\right.$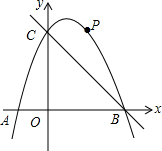 如图,在平面直角坐标系中,二次函数y=-x2+bx+c的图象与x轴交于A、B两点,与y轴交于C(0,3),A点在原点的左侧,B点的坐标为(3,0).点P是抛物线上一个动点,且在直线BC的上方.
如图,在平面直角坐标系中,二次函数y=-x2+bx+c的图象与x轴交于A、B两点,与y轴交于C(0,3),A点在原点的左侧,B点的坐标为(3,0).点P是抛物线上一个动点,且在直线BC的上方.


