题目内容
18.若关于x的不等式$\frac{2x+m}{3}$≥1有4个负整数解,则m的取值范围是-5≤m<13.分析 先把m当作已知条件求出x的取值范围,再根据不等式有4个负整数解即可得出m的取值范围.
解答 解:解不等式$\frac{2x+m}{3}$≥1得,x≥$\frac{3-m}{2}$,
∵不等式有4个负整数解,
∴不等式的负整数解为:-1,-2,-3,-4,
∴-5<x≤-4
即-5<$\frac{3-m}{2}$≤4,解得-5≤m<13.
故答案为:-5≤m<13.
点评 本题考查的是一元一次不等式的整数解,根据题意得出关于m的不等式是解答此题的关键.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
13.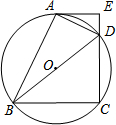 如图,四边形ABCD内接于⊙O,BD是⊙O的直径,过点A作AE⊥CD,交CD的延长线于点E,DA平分∠BDE.
如图,四边形ABCD内接于⊙O,BD是⊙O的直径,过点A作AE⊥CD,交CD的延长线于点E,DA平分∠BDE.
(1)求证:AE是⊙O的切线;
(2)已知AE=8cm,CD=12cm,求⊙O的半径.
 如图,四边形ABCD内接于⊙O,BD是⊙O的直径,过点A作AE⊥CD,交CD的延长线于点E,DA平分∠BDE.
如图,四边形ABCD内接于⊙O,BD是⊙O的直径,过点A作AE⊥CD,交CD的延长线于点E,DA平分∠BDE.(1)求证:AE是⊙O的切线;
(2)已知AE=8cm,CD=12cm,求⊙O的半径.
8.2的平方根是( )
| A. | ±$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | ±1.414 | D. | 4 |
 如图,点P为?ABCD的对角线BD上任意一点,猜想S△BPC和S△ABP的大小关系.并说明理由.
如图,点P为?ABCD的对角线BD上任意一点,猜想S△BPC和S△ABP的大小关系.并说明理由.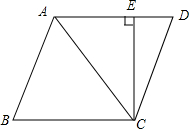 如图,AC是?ABCD的对角线,CE⊥AD,垂足为点E.
如图,AC是?ABCD的对角线,CE⊥AD,垂足为点E.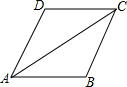 如图,在四边形ABCD中,∠B=∠D,∠DCA=∠CAB,求证:四边形ABCD是平行四边形.
如图,在四边形ABCD中,∠B=∠D,∠DCA=∠CAB,求证:四边形ABCD是平行四边形.