Question

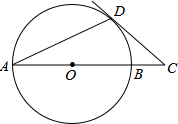
1．（1）解二元一次方程组$\left\{\begin{array}{l}{2x-y=4}\\{3x+y=1}\end{array}\right.$
（2）如图，AB是⊙O的直径，点C在AB的延长线上，CD切⊙O于点D，连接AD．若∠A=25°，则∠C的度数．

Answer 1

分析 （1）利用加减消元法求出解即可；
（2）连接OD，由CD为圆O的切线，利用切线的性质得到OD垂直于CD，根据OA=OD，利用等边对等角得到∠A=∠ODA，求出∠ODA的度数，再由∠COD为△AOD外角，求出∠COD度数，即可确定出∠C的度数．

解答 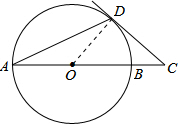解：（1）$\left\{\begin{array}{l}{2x-y=4①}\\{3x+y=1②}\end{array}\right.$，
①+②得：5x=5，
∴x=1，
把x=1代入①得，y=-2，
∴方程组的解为$\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$；

（2）连接OD，
∵CD与圆O相切，
∴OD⊥DC，
∵OA=OD，
∴∠A=∠ODA=25°，
∵∠COD为△AOD的外角，
∴∠COD=50°，
∴∠C=90°-50°=40°．

点评 此题考查了解二元一次方程组，切线的性质，等腰三角形的性质，以及外角性质，熟练掌握切线的性质是解本题的关键．