题目内容
10.先化简再求值:($\frac{x+1}{x-1}+$$\frac{1}{{x}^{2}-2x+1}$)$÷\frac{x}{x-1}$,其中x=$\frac{1}{2}$.分析 原式括号中两边通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把x的值代入计算即可求出值.
解答 解:原式=$\frac{(x+1)(x-1)+1}{(x-1)^{2}}$•$\frac{x-1}{x}$
=$\frac{{x}^{2}}{(x-1)^{2}}$•$\frac{x-1}{x}$
=$\frac{x}{x-1}$
当x=$\frac{1}{2}$时,
原式=-1.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
1.下列命题中的真命题是( )
| A. | 两个矩形一定相似 | |
| B. | 两个菱形一定相似 | |
| C. | 邻边之比为1:2的两个平行四边形相似 | |
| D. | 有一个角是60°的两个菱形相似 |
5.下列等式从左到右的变形是因式分解的是( )
| A. | 6a2b=3a•2ab | B. | (x+4)(x-4)=x2-16 | ||
| C. | 2ax-2ay=2a(x-y) | D. | 4x2+8x-1=4x(x+2)-1 |
19.下列计算错误的是( )
| A. | $\sqrt{2}$+$\sqrt{8}$=3$\sqrt{2}$ | B. | ($\sqrt{3}$-$\sqrt{2}$)($\sqrt{3}$+$\sqrt{2}$)=1 | C. | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{5}$ | D. | $\frac{{\sqrt{21}}}{{\sqrt{3}}}$=$\sqrt{7}$ |
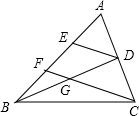 如图,△ABC中,D为AC的中点,E,F为AB的三等分点,且DE∥FC,CF交BD于G,求证:BG=GD.
如图,△ABC中,D为AC的中点,E,F为AB的三等分点,且DE∥FC,CF交BD于G,求证:BG=GD.