题目内容
20.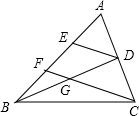 如图,△ABC中,D为AC的中点,E,F为AB的三等分点,且DE∥FC,CF交BD于G,求证:BG=GD.
如图,△ABC中,D为AC的中点,E,F为AB的三等分点,且DE∥FC,CF交BD于G,求证:BG=GD.
分析 由已知条件E,F为AB的三等分点和为AC的中点可证明DE为△ACF的中位线,所以DE∥CF,再由平行线分线段成比例定理即可证明BG=GD.
解答 证明:∵E,F为AB的三等分点,
∴BE=EF=AE=$\frac{1}{3}$AB,
∵AE=$\frac{1}{2}$AF,
∵D为AC的中点,
∴DE为△ACF的中位线,
∴DE∥CF,
∴BG:GD=BF:EF,
∵BF=EF,
∴BG:GD=1,
∴BG=GD.
点评 本题考查了三角形中位线定理的性质以及平行线分线段成比例定理的运用,解题的关键是能够证明DE∥CF.

练习册系列答案
相关题目
15.给出下列三个命题:
(1)有一个角对应相等,且有两条边对应成比例的两个三角形相似;
(2)顶角相等的两个等腰三角形相似;
(3)相等的角是对顶角;
(4)所有的直角三角形都相似,
其中真命题的个数有( )
(1)有一个角对应相等,且有两条边对应成比例的两个三角形相似;
(2)顶角相等的两个等腰三角形相似;
(3)相等的角是对顶角;
(4)所有的直角三角形都相似,
其中真命题的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
12.若$\sqrt{\frac{1}{2-3x}}$在实数范围内有意义,则x的取值范围是( )
| A. | x<$\frac{2}{3}$ | B. | x≤$\frac{2}{3}$ | C. | x≠$\frac{2}{3}$ | D. | x>$\frac{2}{3}$ |
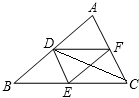 如图所示,在△ABC中,D,E,F分别为边AB,BC,CA的中点,连接DE,DF,CD,EF,请你判断CD和EF的位置关系,并证明.
如图所示,在△ABC中,D,E,F分别为边AB,BC,CA的中点,连接DE,DF,CD,EF,请你判断CD和EF的位置关系,并证明. 如图四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=26cm,点P从点A出发以1cm/s的速度向D运动;点Q从点C同时出发,以3cm/s的速度向点B运动,规定其中一个动点到达端点时,另一个动点也随之停止运动.
如图四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=26cm,点P从点A出发以1cm/s的速度向D运动;点Q从点C同时出发,以3cm/s的速度向点B运动,规定其中一个动点到达端点时,另一个动点也随之停止运动.