题目内容
3. 如图,?ABCD,AE平分∠BAD,交DC的延长线于点E,求证:DA=DE.
如图,?ABCD,AE平分∠BAD,交DC的延长线于点E,求证:DA=DE.
分析 由四边形ABCD为平行四边形,得到对边AB与CD平行,利用两直线平行内错角相等得到一对角相等,再由AE为角平分线得到一对角相等,等量代换后再利用等角对等边即可得证.
解答 证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠E=∠BAE,
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠E=∠DAE,
∴DA=DE.
点评 此题考查了平行四边形的性质,平行线的性质,以及等腰三角形的性质,熟练掌握平行四边形的性质是解本题的关键.

练习册系列答案
相关题目
11.下列性质中,平行四边形不一定具备的是( )
| A. | 邻角互补 | B. | 对角互补 | C. | 对边相等 | D. | 对角线互相平分 |
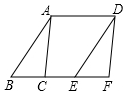 如图,面积为8cm2的△ABC沿BC方向平移至△DEF位置,平移的距离是边BC长的两倍,则图中四边形ACED的面积是24cm2.
如图,面积为8cm2的△ABC沿BC方向平移至△DEF位置,平移的距离是边BC长的两倍,则图中四边形ACED的面积是24cm2.