题目内容
2.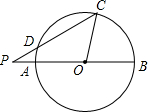 如图,已知AB是⊙O的直径,AB=16,点P是AB所在直线上一点,OP=10,点C是⊙O上一点,PC交⊙O于点D,sin∠BPC=$\frac{3}{5}$,求CD的长.
如图,已知AB是⊙O的直径,AB=16,点P是AB所在直线上一点,OP=10,点C是⊙O上一点,PC交⊙O于点D,sin∠BPC=$\frac{3}{5}$,求CD的长.
分析 过O作OE⊥CD于E,由垂径定理得到CD=2CE,解直角三角形得到OE=OP×sin∠BPC=6,根据勾股定理即可得到结论.
解答 解:过O作OE⊥CD于E,
∴CD=2CE,
∵ AB是⊙O的直径,AB=16,
AB是⊙O的直径,AB=16,
∴OC=8,
∵sin∠BPC=$\frac{3}{5}$,OP=10,
∴OE=OP×sin∠BPC=6,
∴CE=$\sqrt{O{C}^{2}-O{E}^{2}}$=2$\sqrt{7}$,
∴CD=2CE=4$\sqrt{7}$.
点评 本题考查了垂径定理,勾股定理,解直角三角形,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
7.小洪根据演讲比赛中九位评委所给的分数制作了如下表格:
如果去掉一个最高分和一个最低分,那么表格中数据一定不发生变化的是( )
| 平均数 | 中位数 | 众数 | 方差 |
| 8.5 | 8.3 | 8.1 | 0.15 |
| A. | 平均数 | B. | 中位数 | C. | 众数 | D. | 方差 |
14.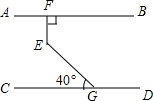 如图,AB∥CD,EF⊥AB于F,∠EGC=40°,则∠FEG=( )
如图,AB∥CD,EF⊥AB于F,∠EGC=40°,则∠FEG=( )
 如图,AB∥CD,EF⊥AB于F,∠EGC=40°,则∠FEG=( )
如图,AB∥CD,EF⊥AB于F,∠EGC=40°,则∠FEG=( )| A. | 120° | B. | 130° | C. | 140° | D. | 150° |
12.下列叙述正确的是( )
| A. | 方差越大,说明数据就越稳定 | |
| B. | 有一个锐角相等的两个直角三角形相似 | |
| C. | 在不等式两边同乘以或同除以一个不为0的数时,不等号的方向不变 | |
| D. | 两边及其一边的对角对应相等的两个三角形全等 |
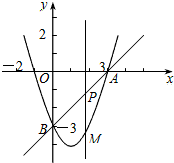 如图,在平面直角坐标系中,抛物线y=x2-2x-3和直线y=x-3经过点A、B,点P是直线AB上的动点,过点P作x轴的垂线交抛物线于点M,设点P的横坐标为t.
如图,在平面直角坐标系中,抛物线y=x2-2x-3和直线y=x-3经过点A、B,点P是直线AB上的动点,过点P作x轴的垂线交抛物线于点M,设点P的横坐标为t.
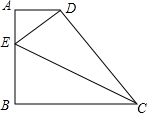 如图,已知梯形ABCD中,AD∥BC,∠B=90°,AD=2,BC=5,E是AB上一点,将△BCE沿着直线CE翻折,点B恰好与D点重合,则BE=$\frac{5}{2}$.
如图,已知梯形ABCD中,AD∥BC,∠B=90°,AD=2,BC=5,E是AB上一点,将△BCE沿着直线CE翻折,点B恰好与D点重合,则BE=$\frac{5}{2}$.