题目内容
19.张老师在一次“探究性学习”课中,作了如下表的设计:(1)按规律填表(n≥2,n为整数).
(2)上表中,每列三个数分别是(4,3,5),(6,8,10),(8,15,17),(10,24,26),…,每组数有何待点?
(3)如果一个直角三角形的两条直角边分别是20,99,你能立即得出它的斜边吗?
(4)根据上述规律,再列举两组勾股数,要求最小数超过10.
| 4 | 6 | 8 | 10 | … | 2n | … |
| 3 | 8 | 15 | 24 | … | … | |
| 5 | 10 | 17 | 26 | … | … |
分析 (1)观察表格,即可求解;
(2)观察表中每列三个数,可知它们都是一组勾股数;
(3)利用勾股定理即可求解;
解答 解:(1)由图表可以得出:
∵n=2时,4=2×2,3=22-1,5=22+1,
n=3时,6=2×3,8=32-1,10=32+1,
n=4时,8=2×4,15=42-1,17=42+1,
n=5时,10=2×5,24=52-1,26=52+1,
∴n=n时,2n,n2-1,n2+1.
填表如下:
| 4 | 6 | 8 | 10 | … | 2n | … |
| 3 | 8 | 15 | 24 | … | n2-1 | … |
| 5 | 10 | 17 | 26 | … | n2+1 | … |
(3)如果一个直角三角形的两条直角边分别是20,99,那么它的斜边是$\sqrt{2{0}^{2}+9{9}^{2}}$=101;
(4)如n=6时,2n=12,n2-1=35,n2+1=37;
n=7时,2n=14,n2-1=48,n2+1=50.
两组勾股数可以是:12,35,37;14,48,50.
点评 本题考查了勾股数:满足a2+b2=c2 的三个正整数,称为勾股数.解题的关键是仔细观察表中的数据,找出规律,进而利用规律解决问题.

练习册系列答案
相关题目
 如图,O为Rt△ABC的直角边AC上一点,以OC为半径的半圆与斜边AB相切于点D,交AC于点E,已知AB=5,AC=4,求BD的长和⊙O的半径.
如图,O为Rt△ABC的直角边AC上一点,以OC为半径的半圆与斜边AB相切于点D,交AC于点E,已知AB=5,AC=4,求BD的长和⊙O的半径. 在平面直角坐标系xOy中,对于点P和⊙O给出如下定义:若⊙O上存在两个点A、B,使得∠APB=60°,则称P为⊙O的关联点.
在平面直角坐标系xOy中,对于点P和⊙O给出如下定义:若⊙O上存在两个点A、B,使得∠APB=60°,则称P为⊙O的关联点.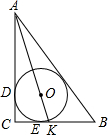 若⊙O为△ABC的内切圆,∠C=90°,AO的延长线交BC于点K,AC=4,CK=1,求内切圆的半径.
若⊙O为△ABC的内切圆,∠C=90°,AO的延长线交BC于点K,AC=4,CK=1,求内切圆的半径. 如图,直线AB与直线CD相交于点O,∠AOC=25°,∠COE=90°,OF是∠COE内一条射线,OE平分∠FOB.
如图,直线AB与直线CD相交于点O,∠AOC=25°,∠COE=90°,OF是∠COE内一条射线,OE平分∠FOB.