题目内容
4.化简:${(\sqrt{1-a})^2}+\sqrt{{{(a-2)}^2}}$=3-2a.分析 首先根据$\sqrt{1-a}$有意义,确定a的取值范围,再应用二次根式的性质进行化简.
解答 解:因为$\sqrt{1-a}$有意义
∴1-a≥0,即a≤1
当a≤1时,|a-2|=2-a
∴原式=1-a+|a-2|
=1-a+2-a
=3-2a.
故答案为:3-2a
点评 本题考查了二次根式有意义的条件,二次根式的化简.二次根式的性质:①双非负性$\sqrt{a}$≥0,a≥0;②$(\sqrt{a})^{2}=a$;③$\sqrt{{a}^{2}}$=|a|;④$\sqrt{ab}=\sqrt{a}×\sqrt{b}$(a≥0,b≥0);⑤$\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}$(a≥0,b>0)

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
15. 如图,数轴上A、B两点分别对着有理数a、b,则下列式子错误的是( )
如图,数轴上A、B两点分别对着有理数a、b,则下列式子错误的是( )
 如图,数轴上A、B两点分别对着有理数a、b,则下列式子错误的是( )
如图,数轴上A、B两点分别对着有理数a、b,则下列式子错误的是( )| A. | a<b | B. | |a|>|b| | C. | a+b>0 | D. | ab<0 |
12.若A和B都是六次多项式则( )
| A. | A+B一定是多项式 | B. | A-B一定是单项式 | ||
| C. | A-B是次数不高于6的整式 | D. | A+B是次数不低于6的整式 |
14.若a2+a-1=0,则a3+2a2+2016的值为( )
| A. | 2015 | B. | 2016 | C. | 2017 | D. | 2018 |
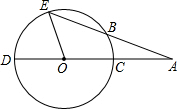 如图,CD是⊙O的直径,∠EOD=72°,AE交⊙O于点B,且AB=OC,则∠A=24°.
如图,CD是⊙O的直径,∠EOD=72°,AE交⊙O于点B,且AB=OC,则∠A=24°.