题目内容
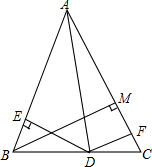 如图,在△ABC中,AB=AC,D为BC上的一点,DE⊥AB于E,DF⊥AC于F,BM为AC边上的高,试探索DE+DF与BM的大小关系.
如图,在△ABC中,AB=AC,D为BC上的一点,DE⊥AB于E,DF⊥AC于F,BM为AC边上的高,试探索DE+DF与BM的大小关系.考点:等腰三角形的性质
专题:
分析:根据S△ABC=S△ABD+S△ACD,利用三角形面积公式即可得出BM=DE+DF.
解答:解:BM=DE+DF.理由如下:
∵S△ABC=S△ABD+S△ACD,
∴
AC×BM=
AB×DE+
AC×DF,
∵AB=AC,
∴BM=DE+DF.
∵S△ABC=S△ABD+S△ACD,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵AB=AC,
∴BM=DE+DF.
点评:本题考查了等腰三角形性质,三角形面积的应用,题目具有一定的代表性,难度适中.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
数轴上表示整数的点称为整点,某数轴的单位长度是1cm,若在这个数轴上任意画一条长为2007cm的线段AB,则线段AB盖住的整点有( )个.
| A、2005或2006 |
| B、2006或2007 |
| C、2007或2008 |
| D、2008或2009 |
 如图,已知AB∥CD,∠α的值为( )
如图,已知AB∥CD,∠α的值为( )| A、145° | B、115° |
| C、85° | D、75° |
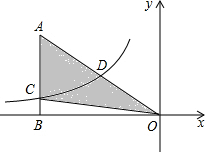 如图,已知反比例函数y=
如图,已知反比例函数y= 如图,在△ABC中,BD、CE分别是边AC、AB上的中线,且BD=CE,求证:AB=AC.
如图,在△ABC中,BD、CE分别是边AC、AB上的中线,且BD=CE,求证:AB=AC.