题目内容
 如图,在△ABC中,BD、CE分别是边AC、AB上的中线,且BD=CE,求证:AB=AC.
如图,在△ABC中,BD、CE分别是边AC、AB上的中线,且BD=CE,求证:AB=AC.考点:全等三角形的判定与性质,等腰三角形的判定与性质,三角形中位线定理,平行四边形的判定与性质
专题:证明题
分析:首先过点D做DF∥EC交BC的延长线与F,连结DE,进而得出四边形DECF是平行四边形,再利用平行四边形的性质得出∠ECB=∠DBC,进而求出△ECB≌△DBC,即可得出答案.
解答: 证明:过点D做DF∥EC交BC的延长线与F,连结DE.
证明:过点D做DF∥EC交BC的延长线与F,连结DE.
∵D、E分别是AC,AB的中点
∴DE∥BC
∵DF∥EC
∴四边形DECF是平行四边形
∴CE=FD
∴∠DBC=∠DFB
∵DF∥BD
∴∠ECB=∠DFB
∴∠ECB=∠DBC
在△ECB和△DBC中,
,
∴△ECB≌△DBC(SAS),
∴∠EBC=∠DCB
∴在△ABC中,有AB=AC.
 证明:过点D做DF∥EC交BC的延长线与F,连结DE.
证明:过点D做DF∥EC交BC的延长线与F,连结DE.∵D、E分别是AC,AB的中点
∴DE∥BC
∵DF∥EC
∴四边形DECF是平行四边形
∴CE=FD
∴∠DBC=∠DFB
∵DF∥BD
∴∠ECB=∠DFB
∴∠ECB=∠DBC
在△ECB和△DBC中,
|
∴△ECB≌△DBC(SAS),
∴∠EBC=∠DCB
∴在△ABC中,有AB=AC.
点评:此题主要考查了平行四边形的性质与判定以及全等三角形的判定与性质,得出∠ECB=∠DBC是解题关键.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
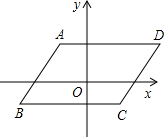 如图,平行四边形ABCD中,AD∥x轴,下列说法正确的是( )
如图,平行四边形ABCD中,AD∥x轴,下列说法正确的是( )| A、A与D的横坐标相同 |
| B、C与D的横坐标相同 |
| C、B与C的纵坐标相同 |
| D、B与D的纵坐标相同 |
比1小2的数是( )
| A、-1 | B、1 | C、3 | D、-2 |
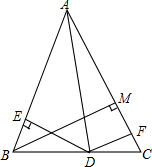 如图,在△ABC中,AB=AC,D为BC上的一点,DE⊥AB于E,DF⊥AC于F,BM为AC边上的高,试探索DE+DF与BM的大小关系.
如图,在△ABC中,AB=AC,D为BC上的一点,DE⊥AB于E,DF⊥AC于F,BM为AC边上的高,试探索DE+DF与BM的大小关系.