题目内容
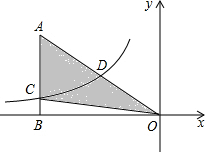 如图,已知反比例函数y=
如图,已知反比例函数y=| k |
| x |
| A、4 | B、2.5 | C、3 | D、2 |
考点:反比例函数系数k的几何意义
专题:
分析:先求出点D的坐标,从而得到反比例函数的解析式,可得出点C的坐标,再利用三角形的面积公式求出△AOC的面积.
解答:解:∵点A的坐标为(-4,2),点D是斜边OA的中点,
∴D(-2,1),把D(-2,1)代入y=
得1=
,解得=-2,
∴反比例函数的解析式为y=
,
∵点C的横坐标为-4,
∴点C的坐标为(-4,
),
∴△AOC的面积=
AC•BO=
×(2-
)×4=3.
故选:C.
∴D(-2,1),把D(-2,1)代入y=
| k |
| x |
| k |
| -2 |
∴反比例函数的解析式为y=
| -2 |
| x |
∵点C的横坐标为-4,
∴点C的坐标为(-4,
| 1 |
| 2 |
∴△AOC的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故选:C.
点评:本题主要考查了反比例函数系数k的几何意义,解题的关键是求出点C的坐标.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
若2a<3a,则a一定满足( )
| A、a>0 | B、a<0 |
| C、a≥0 | D、a≤0 |
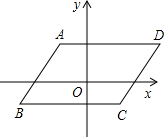 如图,平行四边形ABCD中,AD∥x轴,下列说法正确的是( )
如图,平行四边形ABCD中,AD∥x轴,下列说法正确的是( )| A、A与D的横坐标相同 |
| B、C与D的横坐标相同 |
| C、B与C的纵坐标相同 |
| D、B与D的纵坐标相同 |
在-
,π,0,0.33
四个数中,有理数的个数为( )
| 22 |
| 7 |
| • |
| 3 |
| A、1 | B、2 | C、3 | D、4 |
比1小2的数是( )
| A、-1 | B、1 | C、3 | D、-2 |
 已知四边形AOCD是放置在平面直角坐标系内的梯形,其中O是坐标原点,点A,C,D的坐标分别为(0,8),(5,0),(3,8).若点P在梯形内,且△PAD的面积等于△POC的面积,△PAO的面积等于△PCD的面积.请直接写出点P的坐标
已知四边形AOCD是放置在平面直角坐标系内的梯形,其中O是坐标原点,点A,C,D的坐标分别为(0,8),(5,0),(3,8).若点P在梯形内,且△PAD的面积等于△POC的面积,△PAO的面积等于△PCD的面积.请直接写出点P的坐标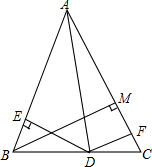 如图,在△ABC中,AB=AC,D为BC上的一点,DE⊥AB于E,DF⊥AC于F,BM为AC边上的高,试探索DE+DF与BM的大小关系.
如图,在△ABC中,AB=AC,D为BC上的一点,DE⊥AB于E,DF⊥AC于F,BM为AC边上的高,试探索DE+DF与BM的大小关系.