题目内容
4.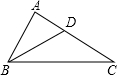 如图,在△ABC中,∠A=90°,BD平分∠ABC,∠C=30°,AD=2,AB=2$\sqrt{3}$,那么S△ABC=6$\sqrt{3}$.
如图,在△ABC中,∠A=90°,BD平分∠ABC,∠C=30°,AD=2,AB=2$\sqrt{3}$,那么S△ABC=6$\sqrt{3}$.
分析 作DE⊥BC于E,根据角平分线的性质得到DE=DA=2,根据直角三角形的性质得到BC=2AB=4$\sqrt{3}$,根据三角形的面积公式计算即可.
解答 解:作DE⊥BC于E,
∵BD平分∠ABC,∠A=90°,DE⊥BC,
∴DE=DA=2,
∵∠A=90°,∠C=30°,
∴BC=2AB=4$\sqrt{3}$,
∴S△ABC=S△ABD+S△DBC=$\frac{1}{2}$×AB×AD+$\frac{1}{2}$×BC×DE=6$\sqrt{3}$,
故答案为:6$\sqrt{3}$.
点评 本题考查的是角平分线的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.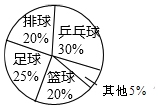 如图是某班学生最喜欢的球类活动人数统计图,则下列说法不正确的是( )
如图是某班学生最喜欢的球类活动人数统计图,则下列说法不正确的是( )
 如图是某班学生最喜欢的球类活动人数统计图,则下列说法不正确的是( )
如图是某班学生最喜欢的球类活动人数统计图,则下列说法不正确的是( )| A. | 该班喜欢乒乓球的学生最多 | |
| B. | 该班喜欢排球和篮球的学生一样多 | |
| C. | 该班喜欢足球的人数是喜欢排球人数的1.25倍 | |
| D. | 该班喜欢其他球类活动的人数为5人 |
19.某班同学毕业时都将自己的照片向全班其他同学各送一张表示留念,全班共送2450张照片,如果全班有x名同学,根据题意,列出方程为( )
| A. | x(x+1)=2450 | B. | x(x-1)=2450 | C. | $\frac{1}{2}$x(x+1)=2450 | D. | $\frac{1}{2}$x(x-1)=2450 |
 如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=2,则△A5B5A6的边长为( )
如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=2,则△A5B5A6的边长为( )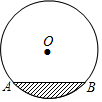 如图,是一圆柱形输水管的横截面,半径为5cm,阴影部分为有水部分,如果水面AB宽为8cm,水面最深地方的高度为2cm.
如图,是一圆柱形输水管的横截面,半径为5cm,阴影部分为有水部分,如果水面AB宽为8cm,水面最深地方的高度为2cm.