题目内容
5. 如图,大正方形的边长为a,小正方形的边长为b,用代数式表示图中阴影部分的面积$\frac{{a}^{2}}{2}$.
如图,大正方形的边长为a,小正方形的边长为b,用代数式表示图中阴影部分的面积$\frac{{a}^{2}}{2}$.
分析 由图形可得,阴影部分的面积是:大正方形面积的一半与小正方形的面积之和减去以(a+b)为底边,高为b的三角形的面积之差再加上以b为底边,高为(a-b)的三角形的面积之和,从而可以解答本题.
解答 解:∵大正方形的边长为a,小正方形的边长为b,
∴图中阴影部分的面积是:$\frac{{a}^{2}}{2}+{b}^{2}-\frac{(a+b)b}{2}+\frac{b×(a-b)}{2}$=$\frac{{a}^{2}}{2}$,
故答案为:$\frac{{a}^{2}}{2}$.
点评 本题考查列代数式,解题的关键是利用数形结合的思想找出所求问题需要的条件.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.在-6,7,8,-$\frac{1}{9}$,12,0,-0.33,$\frac{2}{5}$各数中,负分数的个数有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
14. 如图,梯形ABCD中,AD∥BC,∠B=∠ACD=90°,AB=2,DC=3,则△ABC与△DCA的面积比为( )
如图,梯形ABCD中,AD∥BC,∠B=∠ACD=90°,AB=2,DC=3,则△ABC与△DCA的面积比为( )
 如图,梯形ABCD中,AD∥BC,∠B=∠ACD=90°,AB=2,DC=3,则△ABC与△DCA的面积比为( )
如图,梯形ABCD中,AD∥BC,∠B=∠ACD=90°,AB=2,DC=3,则△ABC与△DCA的面积比为( )| A. | 2:3 | B. | $\sqrt{2}$:$\sqrt{3}$ | C. | 2:5 | D. | 4:9 |
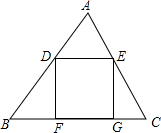 如图,在△ABC中,BC=12,AB=8$\sqrt{2}$,AC=4$\sqrt{5}$,D是AB边上的动点,DE∥BC交AC边于点E,分别过点D,E作BC边的垂线,垂足分别为,G,设AD=x.
如图,在△ABC中,BC=12,AB=8$\sqrt{2}$,AC=4$\sqrt{5}$,D是AB边上的动点,DE∥BC交AC边于点E,分别过点D,E作BC边的垂线,垂足分别为,G,设AD=x.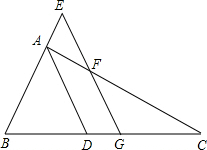 如图,AD为△ABC的角平分线,G为BC中点,GE∥AD,分别交BA的延长线于E,交AC于F,求证:
如图,AD为△ABC的角平分线,G为BC中点,GE∥AD,分别交BA的延长线于E,交AC于F,求证: 如图,在△ABC中,AB⊥EC于点E,∠ABC=45°,BD平分∠ABC且与CE交于点F,BE=a,FE=b,点M,N分别是BD,BC上的动点,当MN+MC最小时,此时动点N与点C的距离为b.
如图,在△ABC中,AB⊥EC于点E,∠ABC=45°,BD平分∠ABC且与CE交于点F,BE=a,FE=b,点M,N分别是BD,BC上的动点,当MN+MC最小时,此时动点N与点C的距离为b.