题目内容
14. 如图,梯形ABCD中,AD∥BC,∠B=∠ACD=90°,AB=2,DC=3,则△ABC与△DCA的面积比为( )
如图,梯形ABCD中,AD∥BC,∠B=∠ACD=90°,AB=2,DC=3,则△ABC与△DCA的面积比为( )| A. | 2:3 | B. | $\sqrt{2}$:$\sqrt{3}$ | C. | 2:5 | D. | 4:9 |
分析 由AD∥BC,得出∠ACB=∠DAC,证得△ABC∽△DCA,再由面积的比等于相似比的平方,即可得出结论.
解答 解:∵AD∥BC,
∴∠ACB=∠DAC
又∵∠B=∠ACD=90°,
∴△CBA∽△ACD
∴$\frac{BC}{AC}$=$\frac{AC}{AD}$=$\frac{AB}{DC}$=$\frac{2}{3}$,
∴$\frac{{S}_{△ABC}}{{S}_{△DCA}}$=$\frac{B{C}^{2}}{A{C}^{2}}$=$\frac{4}{9}$,
∴△ABC与△DCA的面积比为4:9.
故选:D.
点评 本题考查了梯形的性质、相似三角形的判定与性质;通过证明三角形相似得出面积比等于相似比的平方是解决问题的关键.

练习册系列答案
相关题目
19.抛物线y=x2-x-1与坐标轴的交点个数是( )
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
4.下列说法正确的是( )
| A. | 中非峰会,中国政府承诺向非洲提供总额600亿美元的资金支持其发展,将600亿用科学记数法表示为6×1011 | |
| B. | 在一个只装有白球和红球的袋中摸球,摸出红球是必然事件 | |
| C. | 在比例尺为1:100000的地图上,量得甲、乙两地的距离是15cm,则两地的实际距离是15km | |
| D. | 任意三角形都有外接圆和内切圆,它们是同心圆 |
 如图,大正方形的边长为a,小正方形的边长为b,用代数式表示图中阴影部分的面积$\frac{{a}^{2}}{2}$.
如图,大正方形的边长为a,小正方形的边长为b,用代数式表示图中阴影部分的面积$\frac{{a}^{2}}{2}$.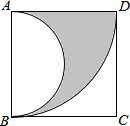 如图,在边长为2的正方形ABCD中,先以点A为圆心,AD的长为半径画弧,再以AB边的中点为圆心,AB长的一半为半径画弧,则两弧之间的阴影部分面积是$\frac{1}{2}π$结果保留π).
如图,在边长为2的正方形ABCD中,先以点A为圆心,AD的长为半径画弧,再以AB边的中点为圆心,AB长的一半为半径画弧,则两弧之间的阴影部分面积是$\frac{1}{2}π$结果保留π).