题目内容
15.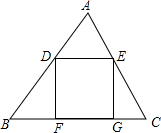 如图,在△ABC中,BC=12,AB=8$\sqrt{2}$,AC=4$\sqrt{5}$,D是AB边上的动点,DE∥BC交AC边于点E,分别过点D,E作BC边的垂线,垂足分别为,G,设AD=x.
如图,在△ABC中,BC=12,AB=8$\sqrt{2}$,AC=4$\sqrt{5}$,D是AB边上的动点,DE∥BC交AC边于点E,分别过点D,E作BC边的垂线,垂足分别为,G,设AD=x.(1)用含x的代数式表示正方形DEFG的面积;
(2)若一个矩形的一边是另一边的2倍,则称这个矩形为方形.矩形DEGF能是方形吗?若能,求其面积;若不能,请说明理由.
分析 (1)由DE∥BC,得到△ADE∽△ABC,根据相似三角形的性质得到$\frac{DE}{BC}$=$\frac{AD}{AB}$,即$\frac{DE}{12}=\frac{x}{8\sqrt{2}}$,即可求得结论;
(2)过A作AH⊥BC于H,根据勾股定理列方程求得BH=8,AH=8,根据前述三角形的性质得到$\frac{BD}{AB}=\frac{DF}{AH}$,求得DF=$\frac{16-\sqrt{2}x}{2}$,当DE=2DF时,求得DE=$\frac{64}{7}$,DF=$\frac{32}{7}$,于是得到S正方形DFGE=$\frac{2048}{49}$,当DF=2DE时,即$\frac{16-\sqrt{2}x}{7}$=2×$\frac{3\sqrt{2}x}{4}$,求得DE=$\frac{24}{23}$,DF=$\frac{48}{23}$,于是得到S正方形DFGE=$\frac{1052}{529}$.
解答 解:(1)∵DE∥BC,
∴△ADE∽△ABC,
∴$\frac{DE}{BC}$=$\frac{AD}{AB}$,即$\frac{DE}{12}=\frac{x}{8\sqrt{2}}$,
解得:DE=$\frac{3\sqrt{2}x}{4}$,
∴正方形DEFG的面积=DE2=$\frac{3}{8}$x2;
(2)过A作AH⊥BC于H,
∴AB2-BH2=AC2-CH2,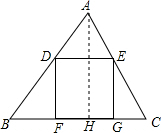
即(8$\sqrt{2}$)2-BH2=(4$\sqrt{5}$)2-(12-BH)2,
∴BH=8,
∴AH=8,
∵DF∥AH,
∴△BDF∽△ABH,
∴$\frac{BD}{AB}=\frac{DF}{AH}$,
∴$\frac{8\sqrt{2}-x}{8\sqrt{2}}$=$\frac{DF}{8}$,
∴DF=$\frac{16-\sqrt{2}x}{2}$,
当DE=2DF时,
即$\frac{3\sqrt{2}x}{4}$=2×$\frac{16-\sqrt{2}x}{2}$,
∴x=$\frac{32\sqrt{2}}{7}$,
∴DE=$\frac{64}{7}$,DF=$\frac{32}{7}$,
∴S正方形DFGE=$\frac{2048}{49}$,
当DF=2DE时,即$\frac{16-\sqrt{2}x}{7}$=2×$\frac{3\sqrt{2}x}{4}$,
∴x=$\frac{16\sqrt{2}}{23}$,
∴DE=$\frac{24}{23}$,DF=$\frac{48}{23}$,
∴S正方形DFGE=$\frac{1052}{529}$.
点评 本题考查了相似三角形的判定与性质、正方形的性质以及面积的计算;本题难度较大,解题的关键是画出图形,注意准确作出辅助线.

 教材全解字词句篇系列答案
教材全解字词句篇系列答案 如图,在墙角O处有个老鼠洞,小猫在A处发现自己的“美餐”--老鼠在B处正往洞口方向逃窜,小猫马上堵截过去.若小猫与老鼠的速度相同,请你在图中画出小猫抓住老鼠的位置P.(保留作图痕迹,不写作法)
如图,在墙角O处有个老鼠洞,小猫在A处发现自己的“美餐”--老鼠在B处正往洞口方向逃窜,小猫马上堵截过去.若小猫与老鼠的速度相同,请你在图中画出小猫抓住老鼠的位置P.(保留作图痕迹,不写作法)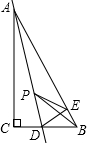 如图,在Rt△ABC中,∠C=90°,AC=4,CB=3,点D是BC边上的点,将△ADC沿直线AD翻折,使点C落在AB边上的点E处,若点P是直线AD上的动点,则△PEB的周长的最小值是4.
如图,在Rt△ABC中,∠C=90°,AC=4,CB=3,点D是BC边上的点,将△ADC沿直线AD翻折,使点C落在AB边上的点E处,若点P是直线AD上的动点,则△PEB的周长的最小值是4. 如图,大正方形的边长为a,小正方形的边长为b,用代数式表示图中阴影部分的面积$\frac{{a}^{2}}{2}$.
如图,大正方形的边长为a,小正方形的边长为b,用代数式表示图中阴影部分的面积$\frac{{a}^{2}}{2}$.