题目内容
16.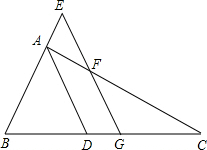 如图,AD为△ABC的角平分线,G为BC中点,GE∥AD,分别交BA的延长线于E,交AC于F,求证:
如图,AD为△ABC的角平分线,G为BC中点,GE∥AD,分别交BA的延长线于E,交AC于F,求证:(1)BE=CF;
(2)CF=$\frac{1}{2}$(AB+AC).
分析 (1)过B作BN‖AC交EG延长线于N点,即可证明BN=CF,然后利用等角对等边证明△BEN是等腰三角形即可;
(2)首先证明AE=AF,然后利用等量代换证明AB+AC=BE+FC即可证得.
解答 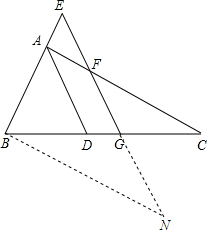 证明:(1)过B作BN‖AC交EG延长线于N点,
证明:(1)过B作BN‖AC交EG延长线于N点,
∵BN‖AC,BG=CG,
∴CF=BN,∠CFG=∠N,
又∵AD‖EG,AD平分∠BAC,
∴∠CFG=∠DAC=∠E,
∴∠E=∠N,
∴BE=BN,
∴BE=CF;
(2)∵∠EFA=∠CFG,
∴∠E=∠EFA,
∴AE=AF,
∴AB+AC=AB+AF+FC=AB+AE+FC=BE+FC,即BE=CF=$\frac{1}{2}$(AB+AC).
点评 本题考查了平行线的性质以及等腰三角形的判定与性质,正确作出辅助线,把证明BE=CF的问题转化为证明△BEN是等腰三角形问题是关键.

练习册系列答案
相关题目
8.计算(-$\frac{3}{2}$a2b)3的结果是( )
| A. | -$\frac{3}{2}$a6b3 | B. | -$\frac{27}{8}$a6b3 | C. | $\frac{27}{8}$a6b3 | D. | -$\frac{27}{8}$a5b3 |
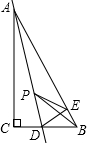 如图,在Rt△ABC中,∠C=90°,AC=4,CB=3,点D是BC边上的点,将△ADC沿直线AD翻折,使点C落在AB边上的点E处,若点P是直线AD上的动点,则△PEB的周长的最小值是4.
如图,在Rt△ABC中,∠C=90°,AC=4,CB=3,点D是BC边上的点,将△ADC沿直线AD翻折,使点C落在AB边上的点E处,若点P是直线AD上的动点,则△PEB的周长的最小值是4. 如图,大正方形的边长为a,小正方形的边长为b,用代数式表示图中阴影部分的面积$\frac{{a}^{2}}{2}$.
如图,大正方形的边长为a,小正方形的边长为b,用代数式表示图中阴影部分的面积$\frac{{a}^{2}}{2}$.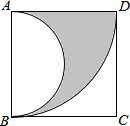 如图,在边长为2的正方形ABCD中,先以点A为圆心,AD的长为半径画弧,再以AB边的中点为圆心,AB长的一半为半径画弧,则两弧之间的阴影部分面积是$\frac{1}{2}π$结果保留π).
如图,在边长为2的正方形ABCD中,先以点A为圆心,AD的长为半径画弧,再以AB边的中点为圆心,AB长的一半为半径画弧,则两弧之间的阴影部分面积是$\frac{1}{2}π$结果保留π).