题目内容
20. 如图,在△ABC中,AB⊥EC于点E,∠ABC=45°,BD平分∠ABC且与CE交于点F,BE=a,FE=b,点M,N分别是BD,BC上的动点,当MN+MC最小时,此时动点N与点C的距离为b.
如图,在△ABC中,AB⊥EC于点E,∠ABC=45°,BD平分∠ABC且与CE交于点F,BE=a,FE=b,点M,N分别是BD,BC上的动点,当MN+MC最小时,此时动点N与点C的距离为b.
分析 根据两点之间线段最短可知:当M与F重合,N点是E点关于BD的对称点时,MN+MC值最小,此时MN+MC=CE,作FN′⊥BC于N′,证得CN′=FN′,然后根据角平分线的性质求得EF=FN′=b,即可求得当MN+MC最小时动点N与点C的距离为b.
解答 解:根据两点之间线段最短可知:当M与F重合,N点是E点关于BD的对称点时,MN+MC值最小,此时MN+MC=CE,
作FN′⊥BC于N′,
∵AB⊥EC于点E,∠ABC=45°,
∴∠BCE=45°,
∴△FN′C是等腰直角三角形,
∴CN′=FN′,
∵BD平分∠ABC,FE⊥AB,FN′⊥BC,
∴EF=FN′=b,
∴CN′=b,
∴当MN+MC最小时动点N与点C的距离为b.
故答案为b.
点评 此题主要考查轴对称--最短路线问题,等腰直角三角形的判断判定和性质,角平分线的性质,熟知两点之间线段最短是解答此题的关键.

练习册系列答案
相关题目
8.计算(-$\frac{3}{2}$a2b)3的结果是( )
| A. | -$\frac{3}{2}$a6b3 | B. | -$\frac{27}{8}$a6b3 | C. | $\frac{27}{8}$a6b3 | D. | -$\frac{27}{8}$a5b3 |
 如图,大正方形的边长为a,小正方形的边长为b,用代数式表示图中阴影部分的面积$\frac{{a}^{2}}{2}$.
如图,大正方形的边长为a,小正方形的边长为b,用代数式表示图中阴影部分的面积$\frac{{a}^{2}}{2}$.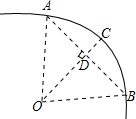 如图,一条公路的转弯处是一段圆弧(图中的弧AB),点O是这段弧的圆心,C是弧AB上一点,OC⊥AB,垂足为D.若这段弯路的半径是100m,CD=20m,则A、B两点的直线距离是( )
如图,一条公路的转弯处是一段圆弧(图中的弧AB),点O是这段弧的圆心,C是弧AB上一点,OC⊥AB,垂足为D.若这段弯路的半径是100m,CD=20m,则A、B两点的直线距离是( ) 将三个数-$\sqrt{3}$,$\sqrt{7}$,$\sqrt{17}$表示在数轴上,被如图所示的墨迹覆盖的数是$\sqrt{7}$.
将三个数-$\sqrt{3}$,$\sqrt{7}$,$\sqrt{17}$表示在数轴上,被如图所示的墨迹覆盖的数是$\sqrt{7}$.