题目内容
12. 如图,线段AB的长为5,C为线段AB上一动点(与点A、B不重合),分别以AC、BC为斜边在AB的同侧作等腰直角三角形ACD和BCE,若AD=x,BE=y,那么x2+y2最小值是$\frac{25}{4}$.
如图,线段AB的长为5,C为线段AB上一动点(与点A、B不重合),分别以AC、BC为斜边在AB的同侧作等腰直角三角形ACD和BCE,若AD=x,BE=y,那么x2+y2最小值是$\frac{25}{4}$.
分析 由等腰直角三角形的性质可用BC把DE2表示出来,再利用二次函数的性质可求得答案.
解答 解:
在等腰RT△ACD和等腰RT△CBE中AD=CD,CE=BE,∠ACD=∠A=45°,∠ECB=∠B=45°
∴∠DCE=90°
∴AD2+CD2=AC2,CE2+BE2=CB2
∴CD2=$\frac{1}{2}$AC2,CE2=$\frac{1}{2}$CB2,
∴DE2=DC2+EC2=$\frac{1}{2}$AC2+$\frac{1}{2}$CB2=$\frac{1}{2}$(AC+BC)2-AC•BC=$\frac{25}{2}$-BC(5-BC)=BC2-5BC+$\frac{25}{2}$=(BC-$\frac{5}{2}$)2+$\frac{25}{4}$,
∴当CB=$\frac{5}{2}$时,DE2有最小值的值最小,
即x2+y2的最小值为$\frac{25}{4}$,
故答案为:$\frac{25}{4}$.
点评 本题主要考查等腰直角三角形的性质,由条件确定出DE2取最小值时的条件是解题的关键

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目

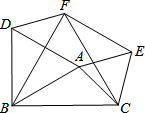 如图,在△ABC中,AB=2,AC=$\sqrt{2}$,∠BAC=105°,△ABD、△ACE、△BCF都是等边三角形,则四边形AEFD的面积为2.
如图,在△ABC中,AB=2,AC=$\sqrt{2}$,∠BAC=105°,△ABD、△ACE、△BCF都是等边三角形,则四边形AEFD的面积为2. 如图,在矩形ABCD中,AB=8,BC=12,若点P在AD边上,连接BP、PC,△BPC是以PB为腰的等腰三角形,则PB的长为10或12.
如图,在矩形ABCD中,AB=8,BC=12,若点P在AD边上,连接BP、PC,△BPC是以PB为腰的等腰三角形,则PB的长为10或12.
 如图1,小红家阳台上放置了一个可折叠的晒衣架,如图2是晒衣架的侧面示意图,经测量:OC=OD=126cm,OA=OB=56cm,且AB=32cm,则此时C,D两点间的距离是72cm.
如图1,小红家阳台上放置了一个可折叠的晒衣架,如图2是晒衣架的侧面示意图,经测量:OC=OD=126cm,OA=OB=56cm,且AB=32cm,则此时C,D两点间的距离是72cm.
 如图所示,一条河的两岸有一段是平行的,河宽36米,在河的南岸边每隔几米有一棵树,在北岸边每隔50米有一根电线杆.小丽站在离南岸边24米的点P处看北岸,发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住,并且在这两棵树之间还有三棵树,则每两棵树间的间隔5米.
如图所示,一条河的两岸有一段是平行的,河宽36米,在河的南岸边每隔几米有一棵树,在北岸边每隔50米有一根电线杆.小丽站在离南岸边24米的点P处看北岸,发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住,并且在这两棵树之间还有三棵树,则每两棵树间的间隔5米. 如图,四边形ABCD是矩形,点E是AB上一点,且BE=3AE,AC,DE相交于点F,则S△CDF:SAEF的值为16.
如图,四边形ABCD是矩形,点E是AB上一点,且BE=3AE,AC,DE相交于点F,则S△CDF:SAEF的值为16.