题目内容
10.对于二次函数 y=(x-1)2+2 的图象,下列说法正确的是( )| A. | 开口向下 | B. | 顶点坐标是(-1,2) | C. | 对称轴是x=1 | D. | 与x轴有两个交点 |
分析 由抛物线解析式可求得其开口方向、顶点坐标、对称轴,再结合一元二次方程与函数图象与x轴的交点的关系可求得答案.
解答 解:
∵y=(x-1)2+2,
∴抛物线开口向上,顶点坐标为(1,2),对称轴为x=1,
令y=0可得(x-1)2+2=0,该方程无实数根,
∴抛物线与x轴没有交点,
故选C.
点评 本题主要考查二次函数的性质,掌握二次函数的顶点式是解题的关键,即在y=a(x-h)2+k中,顶点坐标为(h,k),对称轴为x=h.

练习册系列答案
相关题目
18.下列说法错误的是( )
| A. | 正整数和正分数统称正有理数 | B. | 两个无理数相乘的结果可能等于零 | ||
| C. | 正整数,0,负整数统称为整数 | D. | 3.1415926是小数,也是分数 |
15.下列解方程的各种变形中,正确的是( )
| A. | 由5x=4x+1可得4x-5x=1 | B. | 由3(x-1)-2(2x-3)=1可得3x-3-4x-6=1 | ||
| C. | 由$\frac{x+2}{4}$-1=$\frac{2x-3}{6}$可得3(x+2)-1=2(2x-3) | D. | 由$\frac{1}{2}$x=$\frac{1}{4}$可得x=$\frac{1}{2}$ |
19.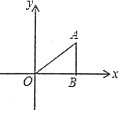 如图.在△ABO中,AB丄OB,OB=$\sqrt{3}$,AB=1,将△ABO绕O点逆时计旋转90°后得到△A1B1O,则点A1的坐标为( )
如图.在△ABO中,AB丄OB,OB=$\sqrt{3}$,AB=1,将△ABO绕O点逆时计旋转90°后得到△A1B1O,则点A1的坐标为( )
 如图.在△ABO中,AB丄OB,OB=$\sqrt{3}$,AB=1,将△ABO绕O点逆时计旋转90°后得到△A1B1O,则点A1的坐标为( )
如图.在△ABO中,AB丄OB,OB=$\sqrt{3}$,AB=1,将△ABO绕O点逆时计旋转90°后得到△A1B1O,则点A1的坐标为( )| A. | (-1,$\sqrt{3}$) | B. | (-1,$\sqrt{3}$)或(1,-$\sqrt{3}$) | C. | (-1,-$\sqrt{3}$) | D. | (-1,-$\sqrt{3}$)或(-$\sqrt{3}$,-1) |
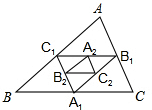 如图,在△ABC中,A1、B1、C1分别是BC、CA、AB的中点,A2、B2、C2分别是B1C1、C1A1、A1B1的中点,…,An、Bn、Cn分别是Bn-1Cn-1、Cn-1An-1、An-1Bn-1的中点,假设△ABC的周长为a,则△A1B1C1的周长为$\frac{1}{2}$a,△A2B2C2的周长为$\frac{1}{4}$a,…,△AnBnCn的周长为$\frac{1}{{2}^{n}}$a.
如图,在△ABC中,A1、B1、C1分别是BC、CA、AB的中点,A2、B2、C2分别是B1C1、C1A1、A1B1的中点,…,An、Bn、Cn分别是Bn-1Cn-1、Cn-1An-1、An-1Bn-1的中点,假设△ABC的周长为a,则△A1B1C1的周长为$\frac{1}{2}$a,△A2B2C2的周长为$\frac{1}{4}$a,…,△AnBnCn的周长为$\frac{1}{{2}^{n}}$a.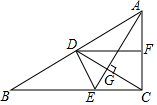 如图,在△ABC中,∠ACB=90°,AE平分∠BAC,CD⊥AE交AE于点G,交AB于点D,DF∥BE交AC于点F.求证:DC平分∠FDE.
如图,在△ABC中,∠ACB=90°,AE平分∠BAC,CD⊥AE交AE于点G,交AB于点D,DF∥BE交AC于点F.求证:DC平分∠FDE.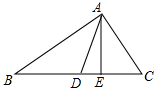 如图,在Rt△ABC中,∠BAC=90°,AD是中线,AE是高,AC=6,AD=5,求AE的长.
如图,在Rt△ABC中,∠BAC=90°,AD是中线,AE是高,AC=6,AD=5,求AE的长.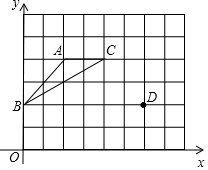 如图,在坐标系的第一象限建立网格,网格中的每个小正方形边长都为1,格点△ABC的顶点坐标分别为A(2,4)、B(0,2)、C(4,4).
如图,在坐标系的第一象限建立网格,网格中的每个小正方形边长都为1,格点△ABC的顶点坐标分别为A(2,4)、B(0,2)、C(4,4).