题目内容
5.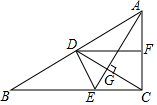 如图,在△ABC中,∠ACB=90°,AE平分∠BAC,CD⊥AE交AE于点G,交AB于点D,DF∥BE交AC于点F.求证:DC平分∠FDE.
如图,在△ABC中,∠ACB=90°,AE平分∠BAC,CD⊥AE交AE于点G,交AB于点D,DF∥BE交AC于点F.求证:DC平分∠FDE.
分析 首先证明AD=AC,推出AE垂直平分线段CD,推出DE=EC,推出∠EDC=∠DCE,由DF∥BC,推出∠FDC=∠DCE,推出∠FDC=∠EDC即可证明.
解答  证明:∵AE⊥CD,
证明:∵AE⊥CD,
∴∠AGD=∠AGC=90°,
∴∠DAG+∠ADG=90°,∠CAG+∠ACG=90°,
∵∠DAG=∠CAG,
∴∠ADG=∠ACG,
∴AD=AC,
∴DG=GC,
∴ED=EC,
∴∠EDC=∠DCE,
∵DF∥BC,
∴∠FDC=∠DCE,
∴∠FDC=∠EDC,
∴CD平分∠FDE.
点评 本题考查直角三角形的性质.角平分线的定义、线段的垂直平分线的判定和性质、平行线的性质等知识,解题的关键是判断AE是线段CD的垂直平分线,属于中考常考题型.

练习册系列答案
 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
13.百度百赚2016年10月24日的万份收益为0.6224元,用四舍五入法按要求对0.6224分别取近似值,其中不正确的是( )
| A. | 精确到个为--1 | B. | 精确到十分位--0.6 | ||
| C. | 精确到0.01--0.63 | D. | 精确到0.001--0,622 |
20.估计$\sqrt{16}$+$\sqrt{20}$的运算结果应在( )
| A. | 6与7之间 | B. | 7与8之间 | C. | 8与9之间 | D. | 9与10之间 |
10.对于二次函数 y=(x-1)2+2 的图象,下列说法正确的是( )
| A. | 开口向下 | B. | 顶点坐标是(-1,2) | C. | 对称轴是x=1 | D. | 与x轴有两个交点 |
17. 如图所示,两个反比例函数y=$\frac{{k}_{1}}{x}$ 和y=$\frac{{k}_{2}}{x}$ 在第一象限内的图象依次是C1和C2,设点P在C1上,PC⊥x轴于点C,交C2于点A,PD⊥y轴于点D,交C2于点B,则四边形PAOB的面积为( )
如图所示,两个反比例函数y=$\frac{{k}_{1}}{x}$ 和y=$\frac{{k}_{2}}{x}$ 在第一象限内的图象依次是C1和C2,设点P在C1上,PC⊥x轴于点C,交C2于点A,PD⊥y轴于点D,交C2于点B,则四边形PAOB的面积为( )
 如图所示,两个反比例函数y=$\frac{{k}_{1}}{x}$ 和y=$\frac{{k}_{2}}{x}$ 在第一象限内的图象依次是C1和C2,设点P在C1上,PC⊥x轴于点C,交C2于点A,PD⊥y轴于点D,交C2于点B,则四边形PAOB的面积为( )
如图所示,两个反比例函数y=$\frac{{k}_{1}}{x}$ 和y=$\frac{{k}_{2}}{x}$ 在第一象限内的图象依次是C1和C2,设点P在C1上,PC⊥x轴于点C,交C2于点A,PD⊥y轴于点D,交C2于点B,则四边形PAOB的面积为( )| A. | k1+k2 | B. | k1-k2 | C. | k1•k2 | D. | k1•k2-k2 |
14.已知点P的坐标为(m,n),若m、n满足(m-n)2=m2+n2-4,则点P所在的象限是( )
| A. | 第一、二象限 | B. | 第二、四象限 | C. | 第二、三象限 | D. | 第一、三象限 |
15.下列各组数值中,是方程2x-y=8的解的是( )
| A. | $\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=2}\\{y=0}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=0.5}\\{y=-7}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=5}\\{y=-2}\end{array}\right.$ |
 如图,在Rt△ABC中,∠ACB=90°,AC=BC=6cm,点P从点A出发,沿AB方向以每秒$\sqrt{2}$cm的速度向终点B运动;同时,动点Q从点B出发,沿BC方向以每秒1cm的速度向终点C运动,当△PQC为以QC为底边的等腰三角形的时候,时间t的值为多少?
如图,在Rt△ABC中,∠ACB=90°,AC=BC=6cm,点P从点A出发,沿AB方向以每秒$\sqrt{2}$cm的速度向终点B运动;同时,动点Q从点B出发,沿BC方向以每秒1cm的速度向终点C运动,当△PQC为以QC为底边的等腰三角形的时候,时间t的值为多少?