题目内容
14．王老师在教学过程中善于把数学知识与实际生活联系在一起．在课堂上，他把全班同学分成五组，编号分别是A、B、C、D、E，每组的人数分别是12、9、11、10、8．游戏规则：当他数完1后，人数最少的那一组学生不动，其他各组各出一个人去人数最少的那组；当他数完2后，此时人数最少的那一组学生不动，其他各组再各出一个人去人数最少的那组…如此进行下去，那么当王老师数完2 016后，A、B、C、D、E五个组中的人数依次是11，8，10，9，12．分析 从数完1后其他各组各出一个人去人数最少的那组后写出每组的对应数，再从数完2后其他各组各出一个人去人数最少的那组后后写出每组的对应数…依此类推找出规律即可解答．
解答 解：A B C D E
第一次 11 8 10 9 12
第二次 10 12 9 8 11
第三次 9 11 8 12 10
第四次 8 10 12 11 9
第五次 12 9 11 10 8
由此可以看出经过五次，每组的人数和原来每一组对应的人数相同，
又∵2016=403×5+1，
∴当王老师数完2016后，A，B，C，D，E五组的人数应跟第1组人数相同，
故答案为：11，8，10，9，12．
点评 本题主要考查数字的变化规律，根据题意得出经过五次，每组的人数和原来每一组对应的人数相同是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
16．
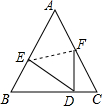如图所示，△ABC是等边三角形，点D为AB上一点，现将△ABC沿EF折叠，使得顶点A与D点重合，且FD⊥BC，则$\frac{AE}{AF}$的值等于（ ）
如图所示，△ABC是等边三角形，点D为AB上一点，现将△ABC沿EF折叠，使得顶点A与D点重合，且FD⊥BC，则$\frac{AE}{AF}$的值等于（ ）| A． | $\frac{4}{3}$ | B． | $\frac{{2\sqrt{3}}}{3}$ | C． | $\frac{{\sqrt{2}+1}}{3}$ | D． | $\frac{{\sqrt{3}+1}}{2}$ |
如图，直线l1，l2分别与另两条直线相交，已知∠1=∠2，求证：∠3+∠4=180°．
如图，在平面直角坐标系中，正方形ABCD的顶点A在y轴正半轴上，顶点B在x轴正半轴上，AC，OD交于点P，其中OA=4，OB=3．
9．
如图，在长方形ABCD中无重叠放入面积分别为16cm2和12cm2的两张正方形纸片，则图中空白部分的面积为（ ）cm2．
如图，在长方形ABCD中无重叠放入面积分别为16cm2和12cm2的两张正方形纸片，则图中空白部分的面积为（ ）cm2．| A． | 16-8$\sqrt{3}$ | B． | -12+8$\sqrt{3}$ | C． | 8-4$\sqrt{3}$ | D． | 4-2$\sqrt{3}$ |
已知：AD是△ABC的角平分线，DE∥AB，DF∥AC，交AB、AC分别为F，E，试判断四边形AFDE是怎样的四边形？证明你的结论．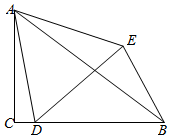
在Rt△ACB中，∠ACB=90°，点D在边BC上，连接AD，以点D为顶点，AD为一边作等边△ADE，连接BE，若BC=7，BE=4，∠CBE=60°，则∠EAB的正切值为$\frac{2\sqrt{3}}{11}$．
如图，已知圆O，弦AB、CD相交于点M．