题目内容
过n边形的一个顶点有7条对角线，m边形有m条对角线，p边形没有对角线，q边形的内角和与外角和相等，求q(n－m)p的值．
500
【解析】分析：若过n边形的一个顶点有7条对角线，则n=10；m边形有m条对角线，即得到方程m(m-3)=m，解得m=5；P边形没有对角线，只有三角形没有对角线，因而P=3；q边形的内角和与外角和相等，内角和与外角和相等的只有四边形，因而q=4．代入代数式就可以求出代数式的值．
本题解析：
∵n边形从一个顶点发出的对角线有n－3条，∴n=7+3=10，
∵m边形有...
练习册系列答案
相关题目
如图所示，在直角梯形ABCD中，AD∥BC，∠B＝90°，AD＝24 ㎝，BC＝26㎝，动点P从点A开始沿AD边以每秒1㎝的速度向D点运动，动点Q从点C开始沿CB边以每秒3㎝的速度向B运动，P，Q分别从A，C同时出发，当其中一点到达端点时，另一点也随之停止运动，设运动时间为t s．
（1）t为何值时，四边形PQCD为平行四边形?
（2）t为何值时，四边形PQCD为等腰梯形?
（3）t为何值时，四边形ABQP为矩形?
（1）t＝6时；（2）t＝7时；（3）t＝时.
【解析】试题分析：（1）要使四边形PQCD是平行四边形，则点在运动的过程中，只需PD=QC就满足题意；
（2）作DE⊥BC，PF⊥BC，垂足分别为E，F，要使四边形PQCD为等腰梯形，则QF＝CE；依此即可求解；
（3）要使四边形ABQP为矩形，则点在运动的过程中，只需AP=BQ就满足题意．
试题解析：【解析】
由已知得AP... 如图，平行四边形ABCD中，E，F分别为边AB，DC的中点，则图中共有平行四边形的个数是 （ ）
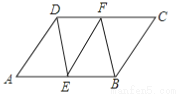
A. 3 B. 4 C. 5 D. 6
B
【解析】【解析】
∵四边形ABCD是平行四边形，∴AB∥CD，AB=CD．
∵E，F分别AB，CD的中点，∴AE=EB=DF=FC，∴四边形AEFD是平行四边形，四边形EFCB是平行四边形，四边形BEDF是平行四边形，∴平行四边形的个数共有4个．故选B． 如果关于x的不等式(3m－1)x＞3m－1的解集为x＜1，那么m的取值范围是( )
A. m＞
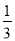B. m＜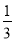
C. m＞－
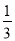D. m＜－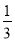
B
【解析】根据一元一次不等式的解法和基本性质，可由关于x的不等式(3m－1)x＞3m－1的解集为x＜1，可知3m-1＜0，解得m＜.
故选：B. 下列不等式变形正确的是（ ）
A．由a＞b，得a﹣2＜b﹣2 B．由a＞b，得|a|＞|b|
C．由a＞b，得﹣2a＜﹣2b D．由a＞b，得a2＞b2
C
【解析】
试题分析：根据不等式两边加（或减）同一个数（或式子），不等号的方向不变；等式两边乘（或除以）同一个正数，不等号的方向不变；不等式两边乘（或除以）同一个负数，不等号的方向改变，可得：
A、等式的两边都减2，不等号的方向不变，故A错误；
B、如a=2，b=﹣3，a＞b，得|a|＜|b|，故B错误；
C、不等式的两边都乘以﹣2，不等号的方向改变，故C正确；
... （10分） 如图所示，求∠A+∠B+∠C+∠D+∠E+∠F的度数．
360°．
【解析】试题分析：连接BE，根据三角形外角的性质可得∠1=∠C+∠D=∠CBE+∠DEB，再由四边形的内角和定理可得∠A+∠ABC+∠C+∠D+∠DEF+∠F=∠A+∠ABC+∠CBE+∠DEB+∠DEF+∠F=∠A+∠ABE+∠BEF+∠F=360°．
试题解析：【解析】
如图，连接BE．
∵∠1=∠C+∠D，∠1=∠CBE+∠DEB，
∴∠C+∠D=∠CB... 如图，在△ABC中，AB＝AC＝5，BC＝8，P是BC边上的动点，过点P作PD⊥AB于点D，PE⊥AC于点E，则PD+PE的长是（ ）
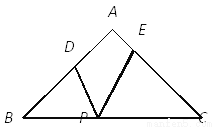
A. 4.8 B. 4.8或3.8 C. 3.8 D. 5
A
【解析】试题分析：作AF⊥BC于F，根据等腰三角形三线合一的性质得出BF=CF=4，然后根据勾股定理求得AF=3，连接AP，根据△ABC的面积=△ABP的面积+△ACP的面积解出答案即可. 分式x-y+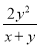
的值为（ ）
A.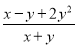 
B. x+y C. 
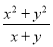D. 以上都不对
C
【解析】试题分析：原式＝
＝
＝．
故选C． 已知平行四边形ABCD中，∠B=4∠A，则∠C=__．
36°
【解析】试题解析：∵四边形BCDA是平行四边形，
∴AD∥CB，∠A=∠C，
∴∠A+∠B=180°，
∵∠B=4∠A，
∴∠A+4∠A=180°，
解得：∠A=36°，
∴∠C=36°.