题目内容
8. 如图,已知AB∥CD∥EF,AF与BE交于O点,若AF=9,BO=2,OC=1,CE=4,求DF和OD的长.
如图,已知AB∥CD∥EF,AF与BE交于O点,若AF=9,BO=2,OC=1,CE=4,求DF和OD的长.
分析 根据AB∥CD∥EF,于是得到$\frac{AD}{DF}=\frac{BC}{CE}$,解方程即可得到DF=$\frac{36}{7}$,由于CD∥EF,于是得到$\frac{OD}{DF}=\frac{OC}{CE}$,解方程得到OD=$\frac{9}{7}$.
解答 解:∵AB∥CD∥EF,
∴$\frac{AD}{DF}=\frac{BC}{CE}$,
即:$\frac{9-DF}{DF}=\frac{2+1}{4}$,
解得:DF=$\frac{36}{7}$,
∵CD∥EF,
∴$\frac{OD}{DF}=\frac{OC}{CE}$,
即:$\frac{OD}{\frac{36}{7}}=\frac{1}{4}$,
∴OD=$\frac{9}{7}$.
点评 本题考查了平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例.平行于三角形的一边,并且和其他两边(或两边的延长线)相交的直线,所截得的三角形的三边与原三角形的三边对应成比例.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.2000×20032003-2003×20002000的值为( )
| A. | 1 | B. | 0 | C. | 2000 | D. | 2003 |
13.下列说法中,错误的是( )
| A. | 两条对角线互相平分的四边形是平行四边形 | |
| B. | 两条对角线相等的四边形是矩形 | |
| C. | 两条对角线互相垂直的矩形形是正方形 | |
| D. | 两条对角线相等的菱形是正方形 |
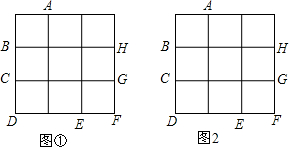 如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点.在正方形网格图①和图②中分别画一个三角形.
如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点.在正方形网格图①和图②中分别画一个三角形.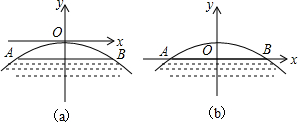
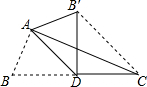 如图,AD是△ABC的中线,∠ADB=45°,△ADB沿直线AD翻折,点B落在B′的位置,BC=2,求B′C的长.
如图,AD是△ABC的中线,∠ADB=45°,△ADB沿直线AD翻折,点B落在B′的位置,BC=2,求B′C的长.