题目内容
18.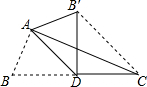 如图,AD是△ABC的中线,∠ADB=45°,△ADB沿直线AD翻折,点B落在B′的位置,BC=2,求B′C的长.
如图,AD是△ABC的中线,∠ADB=45°,△ADB沿直线AD翻折,点B落在B′的位置,BC=2,求B′C的长.
分析 首先根据折叠的性质可得:∠ADB=∠ADB′=45°,即B′D⊥BC,且DB=DB′=CD,由此可得DCB′是个直角边为1的等腰直角三角形,由此得解.
解答 解:∵把△ABC沿直线AD折过来,点B落在B′的位置,
∴△ADB≌△ADB′,
∴∠ADB=∠ADB′=45°,DB=DB′=CD,
∴△DCB′是等腰直角三角形,且直角边为1,
那么斜边B′C=$\sqrt{2}$.
点评 此题主要考查的是图形的翻折变换,能够判断出△DCB′的形状是解答此题的关键.

练习册系列答案
相关题目
9.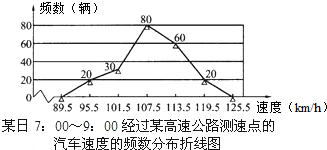 超速行驶是交通事故频发的主要原因之一,交警部门统计某日7:00-9:00经过高速公路某测速点的汽车的速度,得到如下频数分布折线图,若该路段汽车限速110km/h,则超速行驶的汽车有( )
超速行驶是交通事故频发的主要原因之一,交警部门统计某日7:00-9:00经过高速公路某测速点的汽车的速度,得到如下频数分布折线图,若该路段汽车限速110km/h,则超速行驶的汽车有( )
 超速行驶是交通事故频发的主要原因之一,交警部门统计某日7:00-9:00经过高速公路某测速点的汽车的速度,得到如下频数分布折线图,若该路段汽车限速110km/h,则超速行驶的汽车有( )
超速行驶是交通事故频发的主要原因之一,交警部门统计某日7:00-9:00经过高速公路某测速点的汽车的速度,得到如下频数分布折线图,若该路段汽车限速110km/h,则超速行驶的汽车有( )| A. | 20辆 | B. | 60辆 | C. | 70辆 | D. | 80辆 |
6.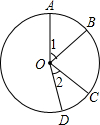 如图,在⊙O中,$\widehat{AB}$=$\widehat{CD}$,∠1=45°,则∠2=( )
如图,在⊙O中,$\widehat{AB}$=$\widehat{CD}$,∠1=45°,则∠2=( )
 如图,在⊙O中,$\widehat{AB}$=$\widehat{CD}$,∠1=45°,则∠2=( )
如图,在⊙O中,$\widehat{AB}$=$\widehat{CD}$,∠1=45°,则∠2=( )| A. | 60° | B. | 30° | C. | 45° | D. | 40° |
3.平面直角坐标系中,点A(-3,2),B(3,4),C(x,y),若AC∥x轴,则线段BC的最小值及此时点C的坐标分别为( )
| A. | 6,(-3,4) | B. | 2,(3,2) | C. | 2,(3,0) | D. | 1,(4,2) |
 如图,已知AB∥CD∥EF,AF与BE交于O点,若AF=9,BO=2,OC=1,CE=4,求DF和OD的长.
如图,已知AB∥CD∥EF,AF与BE交于O点,若AF=9,BO=2,OC=1,CE=4,求DF和OD的长.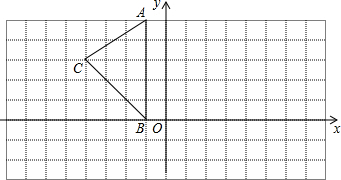 如图,在平面直角坐标系中
如图,在平面直角坐标系中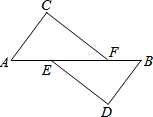 已知,如图:A、E、F、B在一条直线上,AE=BF,∠C=∠B,CF∥DE,
已知,如图:A、E、F、B在一条直线上,AE=BF,∠C=∠B,CF∥DE,